��Ŀ����
2����1���ⲻ��ʽ$\frac{1}{2}$x-1��$\frac{2}{3}$x-$\frac{1}{2}$���������Ľ⼯�������ϱ�ʾ��������2���ⲻ��ʽ��$\left\{\begin{array}{l}{x+1��0}\\{x��\frac{x-2}{3}+2}\end{array}\right.$
��3����֪x=2�ǹ���x�IJ���ʽ3-$\frac{ax}{2}$��3x��һ���⣬��a��ȡֵ��Χ��
���� ��1�����ݽ�һԪһ�β���ʽ�������裺ȥ��ĸ��ȥ���š�����ϲ�ͬ���ϵ����Ϊ1�ɵã�
��2���ֱ����ÿһ������ʽ�Ľ⼯�����ݿھ���ͬ��ȡ��ͬСȡС����СС���м��ҡ����СС����ȷ������ʽ��Ľ⼯��
��3����x=2���벻��ʽ�ɵù���a�IJ���ʽ����֮�ɵã�
��� �⣺��1��ȥ��ĸ���ã�3x-6��4x-3��
����ã�3x-4x��-3+6��
�ϲ�ͬ����ã�-x��3��
ϵ����Ϊ1���ã�x��-3��
��ʾ�����������£�
��2���ⲻ��ʽx+1��0���ã�x��-1��
�ⲻ��ʽx��$\frac{x-2}{3}$+2���ã�x��2��
���ʽ��Ľ⼯Ϊ-1��x��2��
��3����x=2�ǹ���x�IJ���ʽ3-$\frac{ax}{2}$��3x��һ���⣬
��3-a��6��
��ã�a��-3��
���� ���⿼����ǽ�һԪһ�β���ʽ��Ͳ���ʽ��ö��壬��ȷ���ÿһ������ʽ�⼯�ǻ�������֪��ͬ��ȡ��ͬСȡС����СС���м��ң����СС�Ҳ�������ԭ���ǽ�����Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
 ϸ�Ĺ۲�ͼ�����������ʽ��Ȼ�������⣺
ϸ�Ĺ۲�ͼ�����������ʽ��Ȼ�������⣺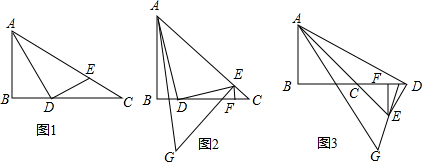

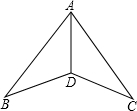 ��ͼ���������һ�Ұ�ֽ����ֱ��������ȵ��߶�AB��AC��Ȼ���������������˶�����Ϊ30��ġ�ABD�͡�ACD���������AD����ʱ���Ͷ϶�AD�ǡ�BAC��ƽ���ߣ���ͬ�����Ľ��������ͬ�⣬��֤���������ͬ�⣬��˵�����ɣ�
��ͼ���������һ�Ұ�ֽ����ֱ��������ȵ��߶�AB��AC��Ȼ���������������˶�����Ϊ30��ġ�ABD�͡�ACD���������AD����ʱ���Ͷ϶�AD�ǡ�BAC��ƽ���ߣ���ͬ�����Ľ��������ͬ�⣬��֤���������ͬ�⣬��˵�����ɣ�