题目内容
17.计算:(1)($\sqrt{6}$+2$\sqrt{8}$)$\sqrt{3}$
(2)$\sqrt{1\frac{2}{3}}$$÷\sqrt{2\frac{1}{3}}$×$\sqrt{1\frac{2}{5}}$
(3)(5$\sqrt{2}$-2$\sqrt{5}$)2
(4)(4$\sqrt{6}$-4$\sqrt{\frac{1}{2}}$+3$\sqrt{8}$)$÷2\sqrt{2}$
(5)$\sqrt{24}$×$\sqrt{\frac{1}{3}}$-4×$\sqrt{\frac{1}{8}}$×$(1-\sqrt{2})^{0}$.
分析 (1)运用乘法分配律展开,化简各二次根式;
(2)将假分数化为带分数,将除法转化为乘法,最后运用二次根式的乘法运算法则计算即可;
(3)运用完全平方公式展开,再计算二次根式的乘方、乘法即可;
(4)化简括号内二次根式同时将除法转化为乘法,运用分配律计算可得;
(5)先运用二次根式的乘法法则计算,在合并同类二次根式即可.
解答 解:(1)原式=($\sqrt{6}+4\sqrt{2}$)×$\sqrt{3}$=3$\sqrt{2}$+4$\sqrt{6}$;
(2)原式=$\sqrt{\frac{5}{3}}÷\sqrt{\frac{7}{3}}$×$\sqrt{\frac{7}{5}}$=$\sqrt{\frac{5}{3}}×\sqrt{\frac{3}{7}}×\sqrt{\frac{7}{5}}$=$\sqrt{\frac{5}{3}×\frac{3}{7}×\frac{7}{5}}$=1;
(3)原式=$(5\sqrt{2})^{2}-2×5\sqrt{2}×2\sqrt{5}+(2\sqrt{5})^{2}$
=50-20$\sqrt{10}$+20
=70-20$\sqrt{10}$;
(4)原式=(4$\sqrt{6}$-2$\sqrt{2}$+6$\sqrt{2}$)×$\frac{\sqrt{2}}{4}$
=2$\sqrt{3}$-1+3
=2$\sqrt{3}$+2;
(5)原式=$\sqrt{24×\frac{1}{3}}$-4×$\frac{\sqrt{2}}{4}$×1
=2$\sqrt{2}$-$\sqrt{2}$
=$\sqrt{2}$.
点评 本题主要考查二次根式的混合运算,在二次根式的混合运算中,要掌握好运算顺序及各运算律是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
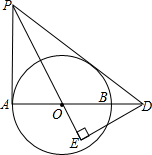 如图,在Rt△PAD中,∠PAD=90°,∠APD的角平分线PO交AD于O点,以O为圆心,OA为半径作⊙O,交AD于点B,过D作DE⊥PO交PO的延长线于点E.
如图,在Rt△PAD中,∠PAD=90°,∠APD的角平分线PO交AD于O点,以O为圆心,OA为半径作⊙O,交AD于点B,过D作DE⊥PO交PO的延长线于点E. 如图,AB为⊙O的直径,点C是⊙O上一点,BD切⊙O于点B,交AC的延长线于点D,点E为$\widehat{AC}$的中点,连接BE交AC于点F.
如图,AB为⊙O的直径,点C是⊙O上一点,BD切⊙O于点B,交AC的延长线于点D,点E为$\widehat{AC}$的中点,连接BE交AC于点F.
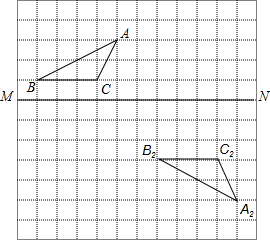 在如图所示的方格纸中.
在如图所示的方格纸中.