��Ŀ����
7�����㣺��1��$\frac{2x}{x-2}+\frac{4}{2-x}$
��2����$\frac{1}{a-b}$-$\frac{b}{{a}^{2}-{b}^{2}}$����$\frac{a}{a+b}$
��3���Ȼ�������ֵ��$\frac{x}{x+2}$��$\frac{{{x^2}-x}}{{{x^2}+4x+4}}$-$\frac{x}{x-1}$������x=1+$\sqrt{3}$��
��4���Ȼ�������ֵ��$\frac{{m}^{2}-2m+1}{{m}^{2}-1}$$�£�m-1-\frac{m-1}{m+1}��$����m=$\sqrt{3}$��
���� ��1�����ݷ�ʽ�ļӷ����Խ���⣻
��2���Ȼ��������ڵ�ʽ�ӣ�Ȼ����ݷ�ʽ�ij������Խ���⣻
��3�����ݷ�ʽ�ij����ͼ������Ի��������ʽ�ӣ�Ȼ��x��ֵ���뼴�ɽ���⣻
��4���Ȼ��������ڵ�ʽ�ӣ�Ȼ����ݷ�ʽ�ij������Ի��������ʽ�ӣ�Ȼ��m��ֵ���뼴�ɽ���⣮
��� �⣺��1��$\frac{2x}{x-2}+\frac{4}{2-x}$
=$\frac{2x-4}{x-2}$
=$\frac{2��x-2��}{x-2}$
=2��
��2����$\frac{1}{a-b}$-$\frac{b}{{a}^{2}-{b}^{2}}$����$\frac{a}{a+b}$
=$\frac{a+b-b}{��a-b����a+b��}��\frac{a+b}{a}$
=$\frac{a}{��a-b����a+b��}��\frac{a+b}{a}$
=$\frac{1}{a-b}$��
��3��$\frac{x}{x+2}$��$\frac{{{x^2}-x}}{{{x^2}+4x+4}}$-$\frac{x}{x-1}$
=$\frac{x}{x+2}��\frac{��x+2��^{2}}{x��x-1��}-\frac{x}{x-1}$
=$\frac{x+2}{x-1}-\frac{x}{x-1}$
=$\frac{2}{x-1}$��
��x=1+$\sqrt{3}$��
ԭʽ=$\frac{2}{1+\sqrt{3}-1}=\frac{2}{\sqrt{3}}=\frac{2\sqrt{3}}{3}$��
��4��$\frac{{m}^{2}-2m+1}{{m}^{2}-1}$$�£�m-1-\frac{m-1}{m+1}��$
=$\frac{��m-1��^{2}}{��m+1����m-1��}��\frac{��m-1����m+1��-��m-1��}{m+1}$
=$\frac{m-1}{m+1}��\frac{m��m-1��}{m+1}$
=$\frac{m-1}{m+1}��\frac{m+1}{m��m-1��}$
=$\frac{1}{m}$��
��m=$\sqrt{3}$ʱ��ԭʽ=$\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$��
���� ���⿼����θ�ʽ�Ļ�����ֵ����ʽ�Ļ�����ֵ������Ĺؼ�����ȷ���ǵļ��㷽����

 ��ͼ����ABC������ΪO������ABC=40�㣬��ACB=72�㣬���BOC��
��ͼ����ABC������ΪO������ABC=40�㣬��ACB=72�㣬���BOC�� ̽������ͼ����ֱ֪��l1��l2��ֱ��l3��ֱ��l1��l2���ڵ�C�͵�D��ֱ��l3��һ��P
̽������ͼ����ֱ֪��l1��l2��ֱ��l3��ֱ��l1��l2���ڵ�C�͵�D��ֱ��l3��һ��P ��ͼ��CD�ֱ�AD��EG�ڵ�D��G��EB�ֱ�AD��EG�ڵ�A��E��AC��EG�ڵ�F��FH��AD�ڵ�H��ADƽ�֡�BAC��EG��AD��CG��EG����C=��AFH��
��ͼ��CD�ֱ�AD��EG�ڵ�D��G��EB�ֱ�AD��EG�ڵ�A��E��AC��EG�ڵ�F��FH��AD�ڵ�H��ADƽ�֡�BAC��EG��AD��CG��EG����C=��AFH��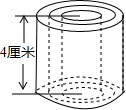 ��ͼ��ʾ��Բ���ĸ���4���ף���Բ������뾶r��cm���仯ʱ��Բ�������V��cm3��Ҳ��֮�仯��
��ͼ��ʾ��Բ���ĸ���4���ף���Բ������뾶r��cm���仯ʱ��Բ�������V��cm3��Ҳ��֮�仯��