题目内容
10.已知不等式(m-1)x>(m-1)(m-2)的解是不等式||x+3|-|x-3||>3的解集的一部分,求m的取值范围.分析 先根据不等式||x+3|-|x-3||>3表示的几何意义,得出x<-$\frac{3}{2}$或x>$\frac{3}{2}$,再分两种情况进行讨论:当m-1>0,即m>1时,x>m-2;当m-1<0,即m<1时,x<m-2,分别求得m的取值范围即可.
解答 解:不等式||x+3|-|x-3||>3表示的几何意义为:在数轴上一点到3和-3的距离之差的绝对值大于3,
①当x≤-3或x≥3时,不等式||x+3|-|x-3||>3成立;
②当-3<x≤0时,不等式||x+3|-|x-3||>3化简得:|x+3+x-3|>3,解得-3<x<-$\frac{3}{2}$;
③当0<x<3时,不等式||x+3|-|x-3||>3化简得:|x+3+x-3|>3,解得$\frac{3}{2}$<x<3;
∴x<-$\frac{3}{2}$或x>$\frac{3}{2}$,
当m-1>0,即m>1时,x>m-2,
∴m-2≥$\frac{3}{2}$,
解得m≥$\frac{7}{2}$(符合题意)
当m-1<0,即m<1时,x<m-2,
∴m-2≤-$\frac{3}{2}$,
解得m≤$\frac{1}{2}$(符合题意).
综上所述,m≤$\frac{1}{2}$或m≥$\frac{7}{2}$.
点评 本题主要考查了不等式的解集,解决问题的关键是利用绝对值的几何意义进行分类讨论.解题时注意:能使不等式成立的未知数的取值范围,叫做不等式的解的集合,简称解集.

练习册系列答案
相关题目
15.已知抛物线y=x2-(2m+1)x+2m不经过第三象限,且当x>2时,函数值y随x的增大而增大,则实数m的取值范围是( )
| A. | 0≤m≤1.5 | B. | m≥1.5 | C. | 0≤m≤1 | D. | 0<m≤1.5 |
19.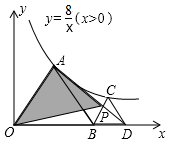 如图,△AOB和△BCD均为等边三角形,且顶点A、C均在双曲线y=$\frac{8}{x}$(x>0),AD与BC相交于点P,则图中△OAP的面积为( )
如图,△AOB和△BCD均为等边三角形,且顶点A、C均在双曲线y=$\frac{8}{x}$(x>0),AD与BC相交于点P,则图中△OAP的面积为( )
 如图,△AOB和△BCD均为等边三角形,且顶点A、C均在双曲线y=$\frac{8}{x}$(x>0),AD与BC相交于点P,则图中△OAP的面积为( )
如图,△AOB和△BCD均为等边三角形,且顶点A、C均在双曲线y=$\frac{8}{x}$(x>0),AD与BC相交于点P,则图中△OAP的面积为( )| A. | 4$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 8 |
 如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=1,则AC的长是2.
如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=1,则AC的长是2.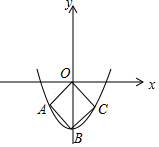 如图,抛物线y=$\frac{1}{2}$x2+c的顶点B在y轴的负半轴上,正方形OABC的两个顶点A,C在抛物线上,则c的值是-4.
如图,抛物线y=$\frac{1}{2}$x2+c的顶点B在y轴的负半轴上,正方形OABC的两个顶点A,C在抛物线上,则c的值是-4.