题目内容
利用二次函数的图象,求下列一元二次方程的近似根.
(1)x2+11x=9;
(2)x2+3x+2=0;
(3)x2+2x-9=0;
(4)x2+3=3x.
(1)x2+11x=9;
(2)x2+3x+2=0;
(3)x2+2x-9=0;
(4)x2+3=3x.
考点:图象法求一元二次方程的近似根
专题:数形结合
分析:(1)画抛物线y=x2+11x和直线y=9,它们的交点的横坐标为所求;
(2)画抛物线y=x2+3x+2,抛物线与x轴的交点的横坐标为所求;
(3)画抛物线y=x2+2x-9,抛物线与x轴的交点的横坐标为所求;
(4)画抛物线y=x2-3x+3,抛物线与x轴没有交点,说明方程没有实数解.
(2)画抛物线y=x2+3x+2,抛物线与x轴的交点的横坐标为所求;
(3)画抛物线y=x2+2x-9,抛物线与x轴的交点的横坐标为所求;
(4)画抛物线y=x2-3x+3,抛物线与x轴没有交点,说明方程没有实数解.
解答:解:(1)如图1:
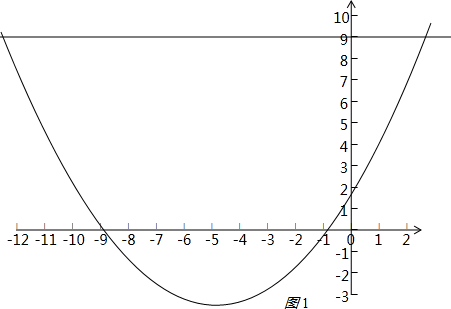
方程的近似根为x1=0.8,x2=-11.8;
(2)如图2:
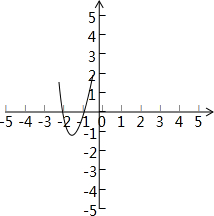
方程的根为x1=-1.0,x2=-2.0;
(3)如图3:
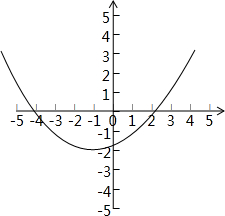
方程的近似根为x1=-4.2,x2=2.2;
(4)如图4:
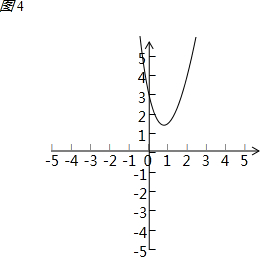
方程没有实数解.

方程的近似根为x1=0.8,x2=-11.8;
(2)如图2:
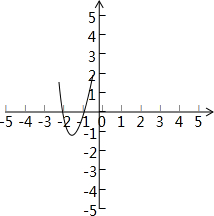
方程的根为x1=-1.0,x2=-2.0;
(3)如图3:
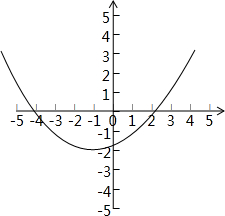
方程的近似根为x1=-4.2,x2=2.2;
(4)如图4:
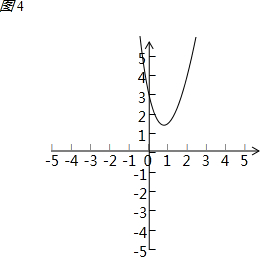
方程没有实数解.
点评:本题考查了利用二次函数图象求一元二次方程的近似根:作出函数的图象,并由图象确定方程的解的个数;由图象与y=h的交点位置确定交点横坐标的范围;观察图象求得方程的根(由于作图或观察存在误差,由图象求得的根一般是近似的.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
在(-1)3,(-1)2012,-22,(-3)2这四个数中,最大的数与最小的数的差等于( )
| A、10 | B、8 | C、5 | D、13 |
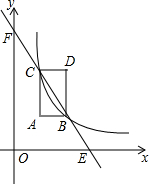 如图,矩形ABDC中,AB∥x轴,AC∥y轴,反比例函数y=
如图,矩形ABDC中,AB∥x轴,AC∥y轴,反比例函数y=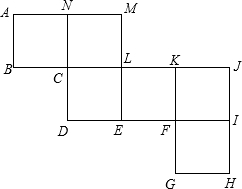 把如图的纸片折叠成一个正方形.
把如图的纸片折叠成一个正方形. 如图:△PQR是等边三角形,∠APB=120°
如图:△PQR是等边三角形,∠APB=120°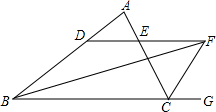 如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=8cm,DE=3cm,求CE的长为
如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=8cm,DE=3cm,求CE的长为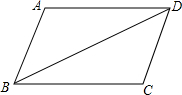 如图,已知:∠ABC=∠ADC,AD∥BC.
如图,已知:∠ABC=∠ADC,AD∥BC.