题目内容
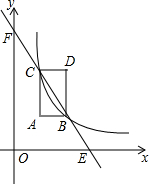 如图,矩形ABDC中,AB∥x轴,AC∥y轴,反比例函数y=
如图,矩形ABDC中,AB∥x轴,AC∥y轴,反比例函数y=| 6 |
| x |
(1)若点A的坐标为(1,2),求矩形ABCD的面积;
(2)在(1)的条件下,判断线段BE与CF的大小关系,并说明理由;
(3)若点A的坐标为(m,n),请直接写出当m,n满足什么关系时,线段CF,CB,BE相等.
考点:反比例函数综合题
专题:
分析:(1)由矩形ABDC中,AB∥x轴,AC∥y轴,点A的坐标为(1,2),则可得点B的纵坐标为2,点C的横坐标为1,又由反比例函数y=
(x>0)的图象过点B,C,即可求得B与C的坐标,继而求得答案;
(2)首先设直线BC的解析式为:y=kx+b,利用待定系数法即可求得其解析式,继而求得E,F的坐标,则可证得BE=CF;
(3)首先延长DC交y轴于点M,延长DB交轴于点N,易证得△FMC∽△CAB∽△BNE,然后由相似三角形的对应边成比例,即可求得答案.
| 6 |
| x |
(2)首先设直线BC的解析式为:y=kx+b,利用待定系数法即可求得其解析式,继而求得E,F的坐标,则可证得BE=CF;
(3)首先延长DC交y轴于点M,延长DB交轴于点N,易证得△FMC∽△CAB∽△BNE,然后由相似三角形的对应边成比例,即可求得答案.
解答:解:(1)∵矩形ABDC中,AB∥x轴,AC∥y轴,点A的坐标为(1,2),
∴点B的纵坐标为2,点C的横坐标为1,
∵反比例函数y=
(x>0)的图象过点B,C,
∴B(3,2),C(1,6),
∴AB=3-1=2,AC=6-2=4,
∴S矩形ABCD=AB•AC=8;
(2)BE=CF.
理由:设直线BC的解析式为:y=kx+b,
把B,C的坐标代入得:
,
解得:
,
∴直线BC的解析式为:y=-2x+8,
∴点E(4,0),点F(0,8),
∴BE=
=
,CF=
=
,
∴BE=CF;
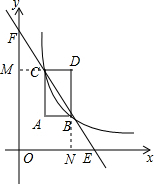 (3)延长DC交y轴于点M,延长DB交轴于点N,
(3)延长DC交y轴于点M,延长DB交轴于点N,
∵矩形ABDC中,AB∥x轴,AC∥y轴,点A的坐标为(m,n),
∴点B的纵坐标为n,点C的横坐标为m,
∵反比例函数y=
(x>0)的图象过点B,C,
∴B(
,n),C(m,
),
∴CM=m,AB=
-m,AC=
-n,BN=n,
∵矩形ABDC中,AB∥x轴,AC∥y轴,
∴∠FMC=∠A=∠BNE=90°,∠FCM=∠CBA=∠BEN,
∴△FMC∽△CAB∽△BNE,
∴
=
,
=
,
∴若CF=CB=BE,
则CM=AB,BN=AC,
∴m=
-m,
-n=n,
∴2mn=6,
即mn=3.
∴当m,n满足mn=3时,线段CF,CB,BE相等.
∴点B的纵坐标为2,点C的横坐标为1,
∵反比例函数y=
| 6 |
| x |
∴B(3,2),C(1,6),
∴AB=3-1=2,AC=6-2=4,
∴S矩形ABCD=AB•AC=8;
(2)BE=CF.
理由:设直线BC的解析式为:y=kx+b,
把B,C的坐标代入得:
|
解得:
|
∴直线BC的解析式为:y=-2x+8,
∴点E(4,0),点F(0,8),
∴BE=
| (4-3)2+(0-2)2 |
| 5 |
| (1-0)2+(6-8)2 |
| 5 |
∴BE=CF;
 (3)延长DC交y轴于点M,延长DB交轴于点N,
(3)延长DC交y轴于点M,延长DB交轴于点N,∵矩形ABDC中,AB∥x轴,AC∥y轴,点A的坐标为(m,n),
∴点B的纵坐标为n,点C的横坐标为m,
∵反比例函数y=
| 6 |
| x |
∴B(
| 6 |
| n |
| 6 |
| m |
∴CM=m,AB=
| 6 |
| n |
| 6 |
| m |
∵矩形ABDC中,AB∥x轴,AC∥y轴,
∴∠FMC=∠A=∠BNE=90°,∠FCM=∠CBA=∠BEN,
∴△FMC∽△CAB∽△BNE,
∴
| CM |
| AB |
| FC |
| BC |
| BN |
| AC |
| BE |
| BC |
∴若CF=CB=BE,
则CM=AB,BN=AC,
∴m=
| 6 |
| n |
| 6 |
| m |
∴2mn=6,
即mn=3.
∴当m,n满足mn=3时,线段CF,CB,BE相等.
点评:此题属于反比例函数综合题,考查了待定系数求函数解析式、正方形的性质以及相似三角形的判定与性质等知识.此题综合性较强,难度较大,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目

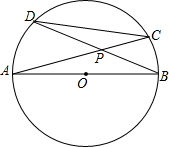 如图,⊙O的直径AB,CD是⊙O的弦,AC与BD相交于点P,若∠BPC=30°,CD=4,求AB.
如图,⊙O的直径AB,CD是⊙O的弦,AC与BD相交于点P,若∠BPC=30°,CD=4,求AB.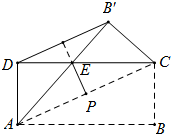 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD相交于点E,连接B′D.若P为AC的中点,求证:PE⊥B′D.
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD相交于点E,连接B′D.若P为AC的中点,求证:PE⊥B′D.