题目内容
 如图:△PQR是等边三角形,∠APB=120°
如图:△PQR是等边三角形,∠APB=120°(1)求证:QR2=AQ•RB;
(2)若AP=2
| 7 |
| 14 |
考点:相似三角形的判定与性质,等边三角形的性质
专题:
分析:(1)证明∠A=∠BPR;进而证明∠B=∠APQ,得到△APQ∽△PBR,列出比例式问题即可解决.
(2)运用△APQ∽△PBR,列出比例式
=
,即可解决问题.
(2)运用△APQ∽△PBR,列出比例式
| PA |
| PB |
| AQ |
| PR |
解答:(1)证明:
∵△PQR为等边三角形,
∴∠QPR=60°,PQ=PR=QR;
又∵∠APB=120°,
∴∠APQ+∠BPR=120°-60°=60°;
而∠PQR=∠A+∠APQ=60°,
∴∠A=∠BPR;
同理可证:∠B=∠APQ,
∴△APQ∽△PBR,
∴
=
,而PQ=PR=QR,
∴QR2=AQ•RB.
(2)
由(1)知:△APQ∽△PBR,
∴
=
,
∴PR=
=
=
,
∴RQ=PR=
.
∵△PQR为等边三角形,
∴∠QPR=60°,PQ=PR=QR;
又∵∠APB=120°,
∴∠APQ+∠BPR=120°-60°=60°;
而∠PQR=∠A+∠APQ=60°,
∴∠A=∠BPR;
同理可证:∠B=∠APQ,
∴△APQ∽△PBR,
∴
| PQ |
| RB |
| AQ |
| PR |
∴QR2=AQ•RB.
(2)
由(1)知:△APQ∽△PBR,
∴
| PA |
| PB |
| AQ |
| PR |
∴PR=
| AQ•PB |
| PA |
2×
| ||
2
|
| 2 |
∴RQ=PR=
| 2 |
点评:该题考查了相似三角形的判定及其性质、等边三角形的性质及其应用等几何知识点问题;解题的关键是灵活运用有关定理来分析、解答.

练习册系列答案
相关题目
 如图:等腰直角△ABC中,若∠ACB=90°,CD=DE=CE,则∠DAB的度数为( )
如图:等腰直角△ABC中,若∠ACB=90°,CD=DE=CE,则∠DAB的度数为( )| A、60° | B、30° |
| C、45° | D、15° |
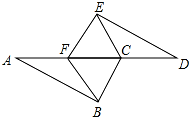 如图,已知AB∥DE,AB=DE,AF=DC,请问图中有
如图,已知AB∥DE,AB=DE,AF=DC,请问图中有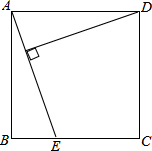 如图,正方形ABCD的面积为10cm2,在边BC上取一点E,连接AE,若AE=4cm,求点D到AE的距离.
如图,正方形ABCD的面积为10cm2,在边BC上取一点E,连接AE,若AE=4cm,求点D到AE的距离.