题目内容
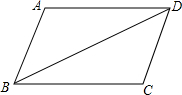 如图,已知:∠ABC=∠ADC,AD∥BC.
如图,已知:∠ABC=∠ADC,AD∥BC.请补充完整过程说明:AB=CD的理由.
证明:∵AD∥BC
∴
∵∠ABC=∠ADC ( 已 知 )
∴
在△ABD和△CDB中
∴△ABD≌△CDB(
∴AB=CD.
考点:全等三角形的判定与性质
专题:推理填空题
分析:根据平行线内错角相等可证∠ADB=∠CBD,进而可以证明∠ABD=∠BDC,即可求证△ABD≌△CDB,即可解题.
解答:证明:∵AD∥BC,
∴∠ADB=∠CBD (两直线平行,内错角相等 )
∵∠ABC=∠ADC ( 已 知 )
∴∠ABD=∠BDC( 等式的性质 )
在△ABD和△CDB中,
,
∴△ABD≌△CDB(ASA)
∴AB=CD.
∴∠ADB=∠CBD (两直线平行,内错角相等 )
∵∠ABC=∠ADC ( 已 知 )
∴∠ABD=∠BDC( 等式的性质 )
在△ABD和△CDB中,
|
∴△ABD≌△CDB(ASA)
∴AB=CD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABD≌△CDB是解题的关键.

练习册系列答案
相关题目
下列“表情图”中,属于轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图:等腰直角△ABC中,若∠ACB=90°,CD=DE=CE,则∠DAB的度数为( )
如图:等腰直角△ABC中,若∠ACB=90°,CD=DE=CE,则∠DAB的度数为( )| A、60° | B、30° |
| C、45° | D、15° |
一元二次方程x2-16=0的解是( )
| A、x1=2,x2=-2 |
| B、x1=4,x2=-4 |
| C、x1=8,x2=-8 |
| D、x1=16,x2=-16 |

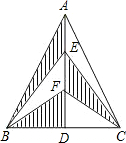 如图,△ABC中,AB=AC,AD⊥BC,点E、F是AD的三等分点,若S△ABC=12m2,则S阴影=
如图,△ABC中,AB=AC,AD⊥BC,点E、F是AD的三等分点,若S△ABC=12m2,则S阴影=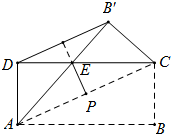 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD相交于点E,连接B′D.若P为AC的中点,求证:PE⊥B′D.
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD相交于点E,连接B′D.若P为AC的中点,求证:PE⊥B′D.