题目内容
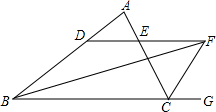 如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=8cm,DE=3cm,求CE的长为
如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=8cm,DE=3cm,求CE的长为考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:根据已知条件,BF、CF分别平分∠ABC、∠ACB的外角,且DE∥BC,可得∠DBF=∠DFB,∠ECF=∠EFC,根据等角对等边得出DF=BD,CE=EF,根据BD-CE=DE即可求得.
解答:解:∵BF、CF分别平分∠ABC、∠ACB的外角,
∴∠DBF=∠CBF,∠FCE=∠FCM,
∵DE∥BC,
∴∠DFB=∠CBF,∠EFC=∠FCM,
∴∠DBF=∠DFB,∠FCE=∠EFC,
∴BD=FD,EF=CE,
∴BD-CE=FD-EF=DE,
∴EF=DF-DE=BD-DE=8-3=5,
∴EC=5cm.
故答案为5.
∴∠DBF=∠CBF,∠FCE=∠FCM,
∵DE∥BC,
∴∠DFB=∠CBF,∠EFC=∠FCM,
∴∠DBF=∠DFB,∠FCE=∠EFC,
∴BD=FD,EF=CE,
∴BD-CE=FD-EF=DE,
∴EF=DF-DE=BD-DE=8-3=5,
∴EC=5cm.
故答案为5.
点评:本题主要考查了等腰三角形的性质以及平行线的性质,利用边角关系并结合等量代换来推导证明是本题的特点.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
下列“表情图”中,属于轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图:等腰直角△ABC中,若∠ACB=90°,CD=DE=CE,则∠DAB的度数为( )
如图:等腰直角△ABC中,若∠ACB=90°,CD=DE=CE,则∠DAB的度数为( )| A、60° | B、30° |
| C、45° | D、15° |
下列比较大小正确的是( )
| A、(-2)3>(-2)2 | ||||
| B、-(-3)>-|-3| | ||||
| C、(-3)3>(-2)3 | ||||
D、-
|
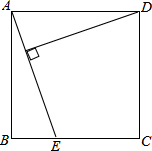 如图,正方形ABCD的面积为10cm2,在边BC上取一点E,连接AE,若AE=4cm,求点D到AE的距离.
如图,正方形ABCD的面积为10cm2,在边BC上取一点E,连接AE,若AE=4cm,求点D到AE的距离.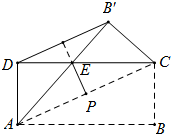 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD相交于点E,连接B′D.若P为AC的中点,求证:PE⊥B′D.
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD相交于点E,连接B′D.若P为AC的中点,求证:PE⊥B′D.