题目内容
13.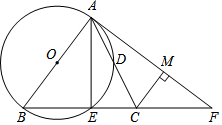 如图,在△ABC中,AB=BC,以AB为直径的⊙O分别交AC,BC于点D,E,过点A作⊙O的切线交BC的延长线于点F,连接AE.
如图,在△ABC中,AB=BC,以AB为直径的⊙O分别交AC,BC于点D,E,过点A作⊙O的切线交BC的延长线于点F,连接AE.(1)求证:∠ABC=2∠CAF;
(2)过点C作CM⊥AF于M点,若CM=4,BE=6,求AE的长.
分析 (1)首先连接BD,由AB为直径,可得∠ADB=90°,然后由等角的余角相等,证得∠1=∠2,继而证得结论;
(2)由圆周角定理,易证得∠2=∠4,又由AB为直径,CM⊥AF,可求得CE=CM=4,继而求得AB的长,则可求得答案.
解答  (1)证明:连接BD,
(1)证明:连接BD,
∵AB是直径,
∴∠ADB=90°,
∵AF是⊙O的切线,
∴∠BAF=90°.
∴∠1+∠BAC=∠2+∠BAC=90°.
∴∠1=∠2.
∵AB=BC,
∴∠ABC=2∠1=2∠2;
(2)解:∵∠1=∠2=∠3,∠3=∠4,
∴∠2=∠4.
∵AB是直径,
∴CE⊥AE,
∵CM⊥AF,CM=4,
∴CE=CM=4,
∵BE=6,
∴AB=BC=BE+EC=10.
在Rt△ABE中,$AE=\sqrt{A{B^2}-B{E^2}}=\sqrt{{{10}^2}-{6^2}}=8$.
点评 此题考查了切线的性质、圆周角定理、勾股定理以及直角三角形的性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
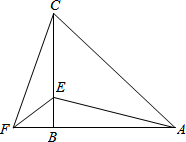 在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.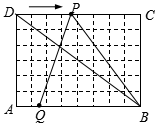 如图1,在6×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动.求运动时间t为多少秒时,△PQB成为以PQ为腰的等腰三角形?
如图1,在6×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动.求运动时间t为多少秒时,△PQB成为以PQ为腰的等腰三角形?
 如图,△ABC向外侧作等腰Rt△ABD与Rt△ACE,∠BAD=∠CAE=90°,F为BC的中点,连接F、A并延长交DE于G点,请问:AF与DE之间存在怎样的数量关系和位置关系?
如图,△ABC向外侧作等腰Rt△ABD与Rt△ACE,∠BAD=∠CAE=90°,F为BC的中点,连接F、A并延长交DE于G点,请问:AF与DE之间存在怎样的数量关系和位置关系? 如图,AB是⊙O的直径,AC、BC是⊙O的弦,∠ACB的平分线交⊙O于D,连接AD、BD,已知AB=6,BC=2.
如图,AB是⊙O的直径,AC、BC是⊙O的弦,∠ACB的平分线交⊙O于D,连接AD、BD,已知AB=6,BC=2.