题目内容
20.在等腰三角形ABC中,AB=AC,AC边上的中线把该三角形的周长分为13.5和11.5两部分,求这个等腰三角形各边的长.分析 因为两个数据具体是哪一部分的不明确,所以分13.5cm是腰长加腰长的一半和11.5cm是腰长加腰长的一半两种情况讨论求解.
解答 解:如图: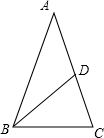
根据题意,
(1)若13.5cm是腰长加腰长的一半,
则腰长为:13.5×$\frac{2}{3}$=9cm,
底边长为:11.5-9×$\frac{1}{2}$=7cm,
此时三角形的三边长为9cm,9cm,7cm,能组成三角形;
(2)若11.5cm是腰长加腰长的一半,
则腰长为:11.5×$\frac{2}{3}$=7$\frac{2}{3}$cm,
底边长为:13.5-$\frac{1}{2}$×7$\frac{2}{3}$=$\frac{29}{3}$cm,
此时三角形的三边长为7$\frac{2}{3}$cm、7$\frac{2}{3}$cm、$\frac{29}{3}$cm,能组成三角形.
故这个三角形各边的长分别为9cm,9cm,7cm,或7$\frac{2}{3}$cm、7$\frac{2}{3}$cm、$\frac{29}{3}$cm.
点评 本题考查了等腰三角形的性质;解题中应用了等腰三角形腰长相等的性质和分类讨论的思想,要注意根据三角形的三边关系判定是否能够组成三角形.

练习册系列答案
相关题目
5.计算.
(1)$\sqrt{4\frac{1}{5}}$+$\sqrt{\frac{7}{10}}$
(2)2$\sqrt{1\frac{1}{2}}$+5$\sqrt{\frac{1}{6}}$.
(1)$\sqrt{4\frac{1}{5}}$+$\sqrt{\frac{7}{10}}$
(2)2$\sqrt{1\frac{1}{2}}$+5$\sqrt{\frac{1}{6}}$.
12.等式$\sqrt{(a-1)^{2}}$=($\sqrt{(1-a)}$)2成立的条件是( )
| A. | 0≤a≤1 | B. | a≤1 | C. | a≥1 | D. | a是非负数 |