题目内容
4.已知a<0,b≤0,c>0,且$\sqrt{{b}^{2}-4ac}$=b-2ac,求b2-4ac的最小值.分析 利用等式的性质将$\sqrt{{b}^{2}-4ac}$=b-2ac两边平方,整理后利用等量代换求出b2-4ac的最小值即可.
解答 解:由$\sqrt{{b}^{2}-4ac}$=b-2ac两边平方得,
b2-4ac=(b-2ac)2,
4a2c2=4abc-4ac,
∵4ac≠0,
∴ac=b-1,
∴b2-4ac=b2-4(b-1)=(b-2)2,
∵b≤0,
∴b2-4ac的最小值为(-2)2=4.
点评 此题主要考查了利用等式的性质、等量代换与非负数的性质解决问题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
19.半径为R的正n边形的边长an等于( )
| A. | 2Rsin$\frac{360°}{n}$ | B. | 2Rsin$\frac{180°}{n}$ | C. | 2Rcos$\frac{360°}{n}$ | D. | 2Rcos$\frac{180°}{n}$ |
13.下列计算一定正确的是( )
| A. | (3x-2)0=1 | B. | π0=0 | C. | (a2-1)0=1 | D. | (x2+2)0=1 |
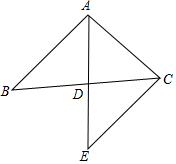 已知:如图,AD是△ABC中BC边上的中线,延长AD到E,使DE=AD.
已知:如图,AD是△ABC中BC边上的中线,延长AD到E,使DE=AD.