题目内容
18.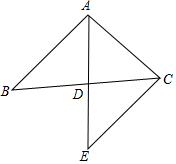 已知:如图,AD是△ABC中BC边上的中线,延长AD到E,使DE=AD.
已知:如图,AD是△ABC中BC边上的中线,延长AD到E,使DE=AD.(1)求证:AB=EC;
(2)试说明AB+AC>2AD的理由;
(3)当AB=6,AC=4时,中线AD的取值范围为1<AD<5.
分析 (1)根据三角形中线的定义可得BD=CD,然后利用“边角边”证明△ABD和△ECD全等,根据全等三角形对应边相等可得AB=EC;
(2)根据三角形的任意两边之和大于第三边可得EC+AC>AE,然后等量代换即可得证;
(3)根据三角形的任意两边之和大于第三边,任意两边之差小于第三边求出AE的取值范围,再除以2即可.
解答 (1)证明:∵AD是△ABC中BC边上的中线,
∴BD=CD,
在△ABD和△ECD中,$\left\{\begin{array}{l}{DE=AD}\\{∠ADB=∠EDC}\\{BD=CD}\end{array}\right.$,
∴△ABD≌△ECD(SAS),
∴AB=EC;
(2)解:由三角形的三边关系得,EC+AC>AE,
∵DE=AD,
∴AE=2AD,
又∵AB=EC,
∴AB+AC>2AD;
(3)解:∵AB=6,
∴EC=6,
又∵AC=4,
∴6-4<AE<6+4,
即2<AE<10,
∵AE=2AD,
∴1<AD<5.
故答案为:1<AD<5.
点评 本题考查了全等三角形的判定与性质,三角形的三边关系,熟练掌握三角形全等的判定方法是解题的关键,本题“遇中线加倍延”的思想要掌握.

练习册系列答案
相关题目
 已知,如图,∠1=∠2,AD⊥BD于D,∠ACB=90°,AC=BC.证明:
已知,如图,∠1=∠2,AD⊥BD于D,∠ACB=90°,AC=BC.证明: 如图所示的平面直角坐标中作函数y=$\frac{4}{3}$x+4的图象,并根据图象求出它与坐标轴所围成图形的周长和面积.
如图所示的平面直角坐标中作函数y=$\frac{4}{3}$x+4的图象,并根据图象求出它与坐标轴所围成图形的周长和面积.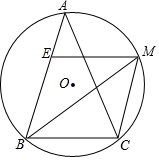 如图,在△ABC中,AB=AC,∠ABC=2∠A,BM平分∠ABC交外接圆于点M,ME∥BC交AB点E.试判断四边形EBCM的形状,并加以证明.
如图,在△ABC中,AB=AC,∠ABC=2∠A,BM平分∠ABC交外接圆于点M,ME∥BC交AB点E.试判断四边形EBCM的形状,并加以证明. 如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点.
如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点. 如图,△ABC的内切圆⊙O与边AB、AC分别切于点D、E,连接DE,∠ABC的平分线BF交直线DE于点F,连接CF,求证:BF⊥CF.
如图,△ABC的内切圆⊙O与边AB、AC分别切于点D、E,连接DE,∠ABC的平分线BF交直线DE于点F,连接CF,求证:BF⊥CF.