题目内容
19.现有1,2,…,48,49这49个连续的正整数,从中选取n个数围成一个圈,如果圈上任意相邻的两个数的乘积都小于100,则n的最大值是( )| A. | 17 | B. | 16 | C. | 18 | D. | 19 |
分析 由题意可知:n取最大值,即让相邻的两个数乘积尽量小,因为2个不同两位数乘积大于100,所以不能相邻,把1位数和两位数相间排列,最多有18个数.
解答 解:100=10×10,
分两种情况:
①把1位数和两位数相间排列,先选1-10这10个数,再在每两个数之间插一个两位数,
即1-49-2-33-3-24-4-19-5-16-6-14-7-12-8-11-9-10,一共18个数,
再如:1-18-2-17-3-16-4-15-5-14-6-13-7-12-8-11-9-10;
②2个不同的两个数相邻,乘积大于100,因此不能相邻;
所以n的最大值是18;
故选C.
点评 本题是数字类变化题,比较复杂,此类题要认真思考,仔细研究,注意理解“圈上任意相邻的两个数的乘积都小于100”,可以从乘积是100的两个因数可以是一位数和两位数或都是两位数考虑,与乘法计算相结合得出结论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.若a2+2a+b2-6b+10=0,则ba的值是( )
| A. | -1 | B. | 3 | C. | -3 | D. | $\frac{1}{3}$ |
8.用配方法解3x2-6x=6配方得( )
| A. | (x-1)2=3 | B. | (x-2)2=3 | C. | (x-3)2=3 | D. | (x-4)2=3 |
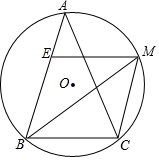 如图,在△ABC中,AB=AC,∠ABC=2∠A,BM平分∠ABC交外接圆于点M,ME∥BC交AB点E.试判断四边形EBCM的形状,并加以证明.
如图,在△ABC中,AB=AC,∠ABC=2∠A,BM平分∠ABC交外接圆于点M,ME∥BC交AB点E.试判断四边形EBCM的形状,并加以证明.