Question

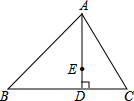如图，△ABC的底边边长BC=a，当顶点A沿BC边上的高AD向点D移动到点E，使DE=

1

2

AE时，△ABC的面积将变为原来的（　　）

• A、

  1

  2

• B、

  1

  3

• C、

  1

  4

• D、

  1

  9

Answer 1

考点：三角形的面积

专题：

分析：根据三角形的面积公式求出变化前与变化后的三角形的面积，然后解答即可．

解答：解：∵DE=

1

2

AE，AD=AE+DE，
∴DE=

1

3

AD，
△ABC原来的面积=

1

2

a•AD，
变化后的面积=

1

2

a•DE=

1

2

a•

1

3

AD，
∴△ABC的面积将变为原来的

1

3

．
故选B．

点评：本题考查了三角形的面积，主要利用了等底的三角形的面积的比等于高线的比，表示出变化前后的三角形的面积是解题的关键．