题目内容
在△ABC中,若∠A,∠B满足|sinA-
|+(cosB-
)2=0,则△ABC是( )
| ||
| 2 |
| 1 |
| 2 |
| A、等腰(非等边)三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、钝角三角形 |
考点:特殊角的三角函数值,非负数的性质:绝对值,非负数的性质:偶次方
专题:
分析:先根据非负数的性质及特殊教的三角函数值∠A和∠B,即可作出判断.
解答:解:根据题意得:sinA-
=0且cosB-
=0,
则sinA=
,cosB=
,
∴∠A=60°,∠B=60°,
∴△ABC是等边三角形.
故选B.
| ||
| 2 |
| 1 |
| 2 |
则sinA=
| ||
| 2 |
| 1 |
| 2 |
∴∠A=60°,∠B=60°,
∴△ABC是等边三角形.
故选B.
点评:本题考查了:①特殊角的三角函数值;②非负数的性质.正确以及特殊角的三角函数值是关键.

练习册系列答案
相关题目
根据下列表格的对应值:
判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解为x的取值范围是( )
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| y=ax2+bx+c | -0.06 | -0.08 | -0.03 | 0.09 |
| A、3<x<3.23 |
| B、3.23<x<3.24 |
| C、3.24<x<3.25 |
| D、3.25<x<3.26 |
在?ABCD中,AB=20,AD=16,AB和CD之间的距离为8,则AD与BC之间的距离为( )
| A、8 | B、9 | C、10 | D、11 |
下列旋转图形中,10°,20°,30°,40°,…,90°,180°都是旋转角度的是( )
| A、正方形 | B、正十边形 |
| C、正二十边形 | D、正三十六边形 |
在下列式子中
①a4+a4=a8;②a6×a4=a24;③a5×b5=(ab)5;④(x3)3=x6;⑤a5÷a5=0;⑥(a-b)2=(b-a)2;⑦(x+y)2=x2+y2;⑧a3÷b3=(
)3.
正确的是( )
①a4+a4=a8;②a6×a4=a24;③a5×b5=(ab)5;④(x3)3=x6;⑤a5÷a5=0;⑥(a-b)2=(b-a)2;⑦(x+y)2=x2+y2;⑧a3÷b3=(
| a |
| b |
正确的是( )
| A、③⑥⑧ | B、①③④⑥ |
| C、③⑥⑦⑧ | D、①③⑥ |
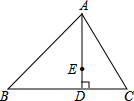 如图,△ABC的底边边长BC=a,当顶点A沿BC边上的高AD向点D移动到点E,使DE=
如图,△ABC的底边边长BC=a,当顶点A沿BC边上的高AD向点D移动到点E,使DE=| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|