题目内容
 如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).(1)求抛物线C1关于原点对称的抛物线C2的解析式;
(2)设抛物线C1的顶点为M,抛物线C2与x轴分别交于C,D两点(点C在点D的左侧),顶点为N,四边形MDNA的面积为S.若点A,点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动;同时,点M,点N以每秒2个单位的速度沿坚直方向分别向下、向上运动,直到点A与点D重合,四点同时停止.求出四边形MDNA的面积S与运动时间t之间的关系式,并写出自变量t的取值范围;当t为何值时,四边形MDNA的面积S有最大值,并求出此最大值.
(3)在运动过程中,四边形MDNA是否能形成矩形?若能,求出此时t的值;若不能,请说明理由.
(4)若P为抛物线C1上的一个点,连接PM,PN,当S△PMN=S矩形MDNA时,过点P作直线PQ∥MN交轴于点Q,则点Q的坐标是多少?直接写出结果.
考点:二次函数综合题
专题:
分析:(1)可先求出A、B、E关于原点对称的对称点的坐标,然后用待定系数法求出抛物线的解析式.
(2)根据中心对称图形的性质不难得出OA=OD,OM=ON,因此四边形AMDN是平行四边形,那么其面积就是三角形ADN面积的2倍,可据此来求S,t的函数关系式.
(3)根据(2)得出的函数的性质和自变量的取值范围即可得出S的最大值及对应的t的值.
(4)此时点Q离MD的距离等于点A到MD的距离的2倍.
(2)根据中心对称图形的性质不难得出OA=OD,OM=ON,因此四边形AMDN是平行四边形,那么其面积就是三角形ADN面积的2倍,可据此来求S,t的函数关系式.
(3)根据(2)得出的函数的性质和自变量的取值范围即可得出S的最大值及对应的t的值.
(4)此时点Q离MD的距离等于点A到MD的距离的2倍.
解答:解:(1)∵C1关于C2原点对称,则有A(-4,0),B(-2,0),E(0,8)
对称点(4,0),(2,0),(0,-8)在抛物线C2上
设抛物线C2的解析式为:y=a(x-4)(x-2)
又当x=0时,y=-8
解得a=-1
∴C2解析式为y=-x2+6x-8;
(2)由中心对称知:
S=2S△AND
而AD=8-2t,AD边上高h=1+2t
∴S=2×
(8-2t)(1+2t)
即S=-4t2+14t+8(0≤t≤4);
由S=-4t2+14t+8=-4(t-
)2+20
∴当t=
时,S最大值=20
;
(3)在转动的过程中,假设四边形MDNA是矩形,连结ON,则有ON=OD,OD=4-t
由勾股定理得:ON2=32+(1+2t)2
∴32+(1+2t)2=(4-t)2
即t2+4t-2=0
解得t1=-2+
t2=-2-
,
又t≥0
∴t=-2+
,
∴当运动了(-2+
)秒时,四边形MDNA为矩形.
(4)∵S△PMN=S矩形MDNA,PQ∥MN,
∴点Q离MD的距离等于点A到MD的距离的2倍.
∵A(-4,0),
∴Q(-8,10).
对称点(4,0),(2,0),(0,-8)在抛物线C2上
设抛物线C2的解析式为:y=a(x-4)(x-2)
又当x=0时,y=-8
解得a=-1
∴C2解析式为y=-x2+6x-8;
(2)由中心对称知:
S=2S△AND
而AD=8-2t,AD边上高h=1+2t
∴S=2×
| 1 |
| 2 |
即S=-4t2+14t+8(0≤t≤4);
由S=-4t2+14t+8=-4(t-
| 7 |
| 4 |
| 1 |
| 4 |
∴当t=
| 7 |
| 4 |
| 1 |
| 4 |
(3)在转动的过程中,假设四边形MDNA是矩形,连结ON,则有ON=OD,OD=4-t
由勾股定理得:ON2=32+(1+2t)2
∴32+(1+2t)2=(4-t)2
即t2+4t-2=0
解得t1=-2+
| 6 |
| 6 |
又t≥0
∴t=-2+
| 6 |
∴当运动了(-2+
| 6 |
(4)∵S△PMN=S矩形MDNA,PQ∥MN,
∴点Q离MD的距离等于点A到MD的距离的2倍.
∵A(-4,0),
∴Q(-8,10).
点评:本题以二次函数为背景,结合动态问题、存在性问题、最值问题,是一道较传统的压轴题,能力要求较高.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是边AD,AB的中点,EF交AC于点H,则
如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是边AD,AB的中点,EF交AC于点H,则 如图,“五一”节,小明和同学一起到游乐场游玩,游乐场的大型摩天轮的半径为20米,旋转1周需要24分钟(匀速).小明乘坐最底部的车厢按逆时针方向旋转(离地面约1米)开始1周的观光.
如图,“五一”节,小明和同学一起到游乐场游玩,游乐场的大型摩天轮的半径为20米,旋转1周需要24分钟(匀速).小明乘坐最底部的车厢按逆时针方向旋转(离地面约1米)开始1周的观光. 如图,AB是圆O的直径,CD⊥AB于D点,AD=4cm,DB=9cm,求CB的长.
如图,AB是圆O的直径,CD⊥AB于D点,AD=4cm,DB=9cm,求CB的长.
 已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接AE.
已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接AE. 用红、黄、绿三种不同的颜色给如图所示的两个小矩形随机涂色,每个矩形涂一种颜色.
用红、黄、绿三种不同的颜色给如图所示的两个小矩形随机涂色,每个矩形涂一种颜色. 如图,A是线段BF延长线上的点,矩形BCDF的外接圆O交AC的中点E.
如图,A是线段BF延长线上的点,矩形BCDF的外接圆O交AC的中点E.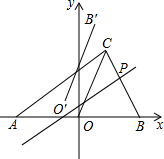 如图,Rt△ABC的斜边AB在x轴上,OA=OB=6,点C在第一象限,∠A=30°,P(m,n)是线段BC上的动点,过点P作BC的垂线a,以直线a为对称轴,将线段OB轴对称变换后得线段O′B′,
如图,Rt△ABC的斜边AB在x轴上,OA=OB=6,点C在第一象限,∠A=30°,P(m,n)是线段BC上的动点,过点P作BC的垂线a,以直线a为对称轴,将线段OB轴对称变换后得线段O′B′,