题目内容
2.欢欢与乐乐两人共同计算(2x+a)(3x+b),欢欢抄错为(2x-a)(3x+b),得到的结果为6x2-13x+6;乐乐抄错为(2x+a)(x+b),得到的结果为2x2-x-6.(1)式子中的a、b的值各是多少?
(2)请计算出原题的正确答案.
分析 (1)根据由于欢欢抄错了第一个多项式中的a符号,得出的结果为6x2-13x+6,可知(2x-a)(3x+b)=6x2+(2b-3a)x-ab=6x2-13x+6,于是2b-3a=-13①;再根据乐乐由于漏抄了第二个多项式中的x的系数,得到的结果为2x2-x-6,可知常数项是-6,可知(2x+a)(x+b)=2x2-x-6,可得到2b+a=-1②,解关于①②的方程组即可求出a、b的值;
(2)把a、b的值代入原式求出整式乘法的正确结果.
解答 解:(1)根据题意可知,由于欢欢抄错了第一个多项式中的a的符号,得到的结果为6x2-13x+6,
那么(2x-a)(3x+b)=6x2+(2b-3a)x-ab=6x2-13x+6,
可得2b-3a=-13 ①
乐乐由于漏抄了第二个多项式中的x的系数,得到的结果为2x2-x-6,
可知(2x+a)(x+b)=2x2-x-6
即2x2+(2b+a)x+ab=2x2-x-6,
可得2b+a=-1 ②,
解关于①②的方程组,可得a=3,b=-2;
(2)正确的式子:
(2x+3)(3x-2)=6x2+5x-6
点评 本题主要是考查多项式的乘法,正确利用法则是正确解决问题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
12.若a>b,则下列式子中错误的是( )
| A. | a-2>b-2 | B. | -2a>-2b | C. | 2a>2b | D. | $\frac{a}{2}$>$\frac{b}{2}$ |
7.|-125|的立方根为( )
| A. | -5 | B. | 5 | C. | 25 | D. | ±5 |
12.对于函数y=$\frac{6}{x}$,下列说法错误的是( )
| A. | 它的图象分布在一、三象限 | B. | 它的图象与直线y=-x无交点 | ||
| C. | 当x<0时,y的值随x的增大而减小 | D. | 当x>0时,y的值随x的增大而增大 |
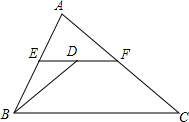 如图,EF为△ABC的中位线,BD平分∠ABC,交EF于D,AB=8,BC=12,则DF的长为2.
如图,EF为△ABC的中位线,BD平分∠ABC,交EF于D,AB=8,BC=12,则DF的长为2. 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-$\frac{1}{2}$x的图象交于A、B两点,若B点的横坐标为2,点P是第二象限内反比例函数图象上的动点,且在直线AB的上方.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-$\frac{1}{2}$x的图象交于A、B两点,若B点的横坐标为2,点P是第二象限内反比例函数图象上的动点,且在直线AB的上方.