题目内容
14.先化简,再求值:($\frac{1}{a-3}$-$\frac{a-2}{{a}^{2}-9}$)•(a+3),其中a=3+2$\sqrt{2}$.分析 先算括号里面的,再算乘法,最后把a的值代入进行计算即可.
解答 解:原式=[$\frac{a+3}{(a-3)(a+3)}$-$\frac{a-2}{(a-3)(a+3)}$]•(a+3)
=$\frac{a+3-a+2}{(a-3)(a+3)}$•(a+3)
=$\frac{5}{a-3}$,
当a=3+2$\sqrt{2}$时,原式=$\frac{5\sqrt{2}}{4}$.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.

练习册系列答案
相关题目
4.已知直线y=kx+b与y=2x-5平行且经过点(1,3),则y=kx+b的表达式是( )
| A. | y=x+2 | B. | y=2x+1 | C. | y=2x+2 | D. | y=2x+3 |
9.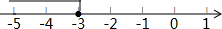 下列不等式中,其解集是如图所示的是( )
下列不等式中,其解集是如图所示的是( )
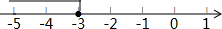 下列不等式中,其解集是如图所示的是( )
下列不等式中,其解集是如图所示的是( )| A. | -x-1≥-2 | B. | -2x-3≥3 | C. | 3x+4≥-5 | D. | x-4≤7 |
4.下列从左到右的变形,属于分解因式的是( )
| A. | (a-3)(a+3)=a2-9 | B. | x2+x-5=x(x+1)-5 | C. | a2+a=a(a+1) | D. | x3y=x•x2•y |
 在下面网格图中,每个小正方形的边长为1,平移△ABC,使点A平移到点D.
在下面网格图中,每个小正方形的边长为1,平移△ABC,使点A平移到点D. 如图,DE∥BC,BE平分∠ABC,求证:∠1=∠3(证明每一步得到的结论,都要写明理由).
如图,DE∥BC,BE平分∠ABC,求证:∠1=∠3(证明每一步得到的结论,都要写明理由). 如图,在△ABC中,D,E,F分别是AB,AC,BC边上的点,且$\frac{AD}{BD}$=$\frac{AE}{CE}$=$\frac{1}{2}$,则四边形ADFE与△ABC的面积之比为$\frac{1}{3}$.
如图,在△ABC中,D,E,F分别是AB,AC,BC边上的点,且$\frac{AD}{BD}$=$\frac{AE}{CE}$=$\frac{1}{2}$,则四边形ADFE与△ABC的面积之比为$\frac{1}{3}$.