题目内容
14.已知△ABC 中,∠A=60°,∠ACB=40°,D为BC边延长线上一点,BM平分∠ABC,E为射线BM上一点.
(1)如图1,连接CE,
①若CE∥AB,求∠BEC的度数;
②若CE平分∠ACD,求∠BEC的度数.
(2)若直线CE垂直于△ABC的一边,请直接写出∠BEC的度数.
分析 (1)①根据三角形的内角和得到∠ABC=80°,由角平分线的定义得到∠ABE=$\frac{1}{2}∠$ABC=40°,根据平行线的性质即可得到结论;
②根据邻补角的定义得到∠ACD=180°-∠ACB=140°,根据角平分线的定义得到∠CBE=$\frac{1}{2}∠$ABC=40°,∠ECD=$\frac{1}{2}$ACD=70°,根据三角形的外角的性质即可得到结论;
(2)①当CE⊥BC时,②如图2,当CE⊥AB于F时,③如图3,当CE⊥AC时,根据垂直的定义和三角形的内角和即可得到结论.
解答 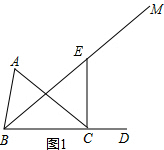 解:(1)①∵∠A=60°,∠ACB=40°,
解:(1)①∵∠A=60°,∠ACB=40°,
∴∠ABC=80°,
∵BM平分∠ABC,
∴∠ABE=$\frac{1}{2}∠$ABC=40°,
∵CE∥AB,
∴∠BEC=∠ABE=40°;
②∵∠A=60°,∠ACB=40°,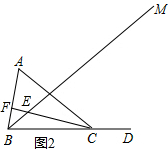
∴∠ABC=80°,∠ACD=180°-∠ACB=140°,
∵BM平分∠ABC,CE平分∠ACD,
∴∠CBE=$\frac{1}{2}∠$ABC=40°,∠ECD=$\frac{1}{2}$ACD=70°,
∴∠BEC=∠ECD-∠CBE=30°;
(2)①如图1,当CE⊥BC时,
∵∠CBE=40°,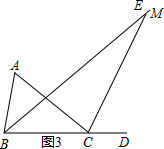
∴∠BEC=50°;
②如图2,当CE⊥AB于F时,
∵∠ABE=40°,
∴∠BEC=90°+40°=130°,
③如图3,当CE⊥AC时,
∵∠CBE=40°,∠ACB=40°,
∴∠BEC=180°-40°-40°-90°=10°.
点评 本题考查了平行线的性质,角平分线的定义,垂直的定义,三角形的内角和,三角形的外角的性质,正确的画出图形是解题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
6.对于同一平面内的三条直线a,b,c,给出下列5个论断:
①a∥b;②b∥c;③a∥c;④a⊥b;⑤a⊥c.
以其中两个论断作为题设,一个论断作为结论,组成一个你认为不正确的命题是( )
①a∥b;②b∥c;③a∥c;④a⊥b;⑤a⊥c.
以其中两个论断作为题设,一个论断作为结论,组成一个你认为不正确的命题是( )
| A. | 已知①②则③ | B. | 已知②⑤则④ | C. | 已知②④则③ | D. | 已知④⑤则② |
4.根据图中的程序,当输入方程x2=2x的解x时,输出结果y=( )


| A. | -4 | B. | 2 | C. | -4或2 | D. | 2或-2 |
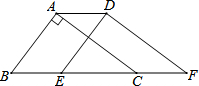 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,将△ABC沿直线BC向右平移2个单位得到△DEF,连接AD,则下列结论①AC∥DF;②ED⊥DF;③四边形ABFD的周长是16.其中正确的个数为( )
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,将△ABC沿直线BC向右平移2个单位得到△DEF,连接AD,则下列结论①AC∥DF;②ED⊥DF;③四边形ABFD的周长是16.其中正确的个数为( )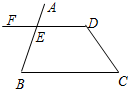 如图,已知∠C+∠D=180°,则∠AED=∠B.完成下面的说理过程.
如图,已知∠C+∠D=180°,则∠AED=∠B.完成下面的说理过程.