题目内容
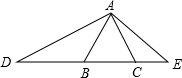如图，△ABC是等边三角形，点D、E分别在CB、BC的延长线上，∠DAE=120°．（1）△ABD与△ECA是否相似？为什么？
（2）若BD=9，CE=4，求BC的长．
考点：相似三角形的判定与性质
专题：
分析：（1）根据相似三角形的性质得到∠DAB+∠EAC=60°，∠E+∠EAC=∠ACB=60°，再根据全等三角形的性质得到∠ABD=∠ACE=120°，从而判断出△ABD∽△ECA．
（2）根据相似三角形的性质列出比例式解答即可．
（2）根据相似三角形的性质列出比例式解答即可．
解答：解：（1）∵△ABC是等边三角形，
∴∠BAC=∠ACB=60°，
∵∠DAE=120°，
∴∠DAB+∠EAC=60°，
又∵∠E+∠EAC=∠ACB=60°，
∴∠DAB=∠EAC，
又∵∠ABD=∠ACE=120°，
∴△ABD∽△ECA．
（2）∵△ABD∽△ECA，
∴
=
，
∴
=
，
解得BC=6．
∴∠BAC=∠ACB=60°，
∵∠DAE=120°，
∴∠DAB+∠EAC=60°，
又∵∠E+∠EAC=∠ACB=60°，
∴∠DAB=∠EAC，
又∵∠ABD=∠ACE=120°，
∴△ABD∽△ECA．
（2）∵△ABD∽△ECA，
∴
| BD |
| AC |
| AB |
| CE |
∴
| 9 |
| BC |
| BC |
| 4 |
解得BC=6．
点评：本题考查了相似三角形的判定和性质，要找到相等的角，并能找到对应边．
练习册系列答案
名校课堂系列答案
相关题目
已知AD⊥BD，BC⊥CD，AB=a cm，BC=b cm，则BD的取值范围是
如图，
如图，直线l的解析式为y=