题目内容
2.平面直角坐标系中,O是坐标原点,点A(1,1)、点B(2,-5),P是y轴上一动点,当△PAB的周长最小时,求∠APO的正切值( )| A. | 2 | B. | 0.5 | C. | -5 | D. | 5 |
分析 先求出点A关于y轴对称的点的坐标,再用待定系数法求出直线A′B的解析式,求出此直线与y轴的交点坐标,再利用三角函数解答即可.
解答 解:∵A(1,1),
∴点A关于y轴对称的点A′(-1,1).
设直线A′B的解析式为y=kx+b(k≠0),
∵B(2,-5),
∴$\left\{\begin{array}{l}{1=-k+b}\\{-5=2k+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2}\\{b=-1}\end{array}\right.$,
∴直线A′B的解析式为y=-2x-1,
当x=0时,y=-1.
∴P(0,-1),
∠APO的正切值=$\frac{1}{1+1}=\frac{1}{2}=0.5$,
故选B
点评 本题考查的是轴对称-最短路线问题,熟知两点之间,线段最短是解答此题的关键.

练习册系列答案
相关题目
14.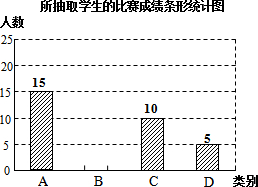 为了提高学生写好汉字的积极性,某校组织全校学生参加汉字听写比赛,比赛成绩从高到低只分A、B、C、D四个等级.若随机抽取该校部分学生的比赛成绩进行统计分析,并绘制了如下的统计图表:
为了提高学生写好汉字的积极性,某校组织全校学生参加汉字听写比赛,比赛成绩从高到低只分A、B、C、D四个等级.若随机抽取该校部分学生的比赛成绩进行统计分析,并绘制了如下的统计图表:
所抽取学生的比赛成绩情况统计表
根据图表的信息,回答下列问题:
(1)本次抽查的学生共有50名;
(2)表中x和m所表示的数分别为:x=20,m=30%,并在图中补全条形统计图;
(3)若该校共有1500名学生,请你估计此次汉字听写比赛有多少名学生的成绩达到B级及B级以上?
 为了提高学生写好汉字的积极性,某校组织全校学生参加汉字听写比赛,比赛成绩从高到低只分A、B、C、D四个等级.若随机抽取该校部分学生的比赛成绩进行统计分析,并绘制了如下的统计图表:
为了提高学生写好汉字的积极性,某校组织全校学生参加汉字听写比赛,比赛成绩从高到低只分A、B、C、D四个等级.若随机抽取该校部分学生的比赛成绩进行统计分析,并绘制了如下的统计图表:所抽取学生的比赛成绩情况统计表
| 成绩等级 | A | B | C | D |
| 人数 | 15 | x | 10 | 5 |
| 抽查学生占抽查 总数的百分比 | m | 40% | 20% | 10% |
(1)本次抽查的学生共有50名;
(2)表中x和m所表示的数分别为:x=20,m=30%,并在图中补全条形统计图;
(3)若该校共有1500名学生,请你估计此次汉字听写比赛有多少名学生的成绩达到B级及B级以上?
12.弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
(1)上表反映了哪些变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体的质量为3kg时,弹簧的长度是多少?
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式.
| 物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
| 弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
(2)当物体的质量为3kg时,弹簧的长度是多少?
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式.
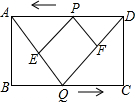 如图,矩形ABCD的边长AB=2cm,BC=5cm,两动点P、Q分别同时从点D、B出发,以1cm/s的速度沿边DA、BC方向向点A、C运动(端点不计),设运动时间为t(s),连接AQ、DQ,过点P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.
如图,矩形ABCD的边长AB=2cm,BC=5cm,两动点P、Q分别同时从点D、B出发,以1cm/s的速度沿边DA、BC方向向点A、C运动(端点不计),设运动时间为t(s),连接AQ、DQ,过点P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.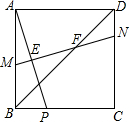 在正方形ABCD中,点P是边BC上一动点(不包含端点),线段AP的垂直平分线与AB、AP、BD、CD分别交于点M、E、F、N.
在正方形ABCD中,点P是边BC上一动点(不包含端点),线段AP的垂直平分线与AB、AP、BD、CD分别交于点M、E、F、N.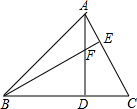 如图,在△ABC中,AD⊥BC,BE⊥AC,AD=BD,求证:BF=AC.
如图,在△ABC中,AD⊥BC,BE⊥AC,AD=BD,求证:BF=AC.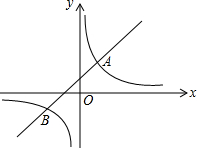 如图,直线y=k1+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(m,2),B(-2,-1)两点.则不等式k1x+b>$\frac{{k}_{2}}{x}$的解集为x>1或-2<x<0.
如图,直线y=k1+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(m,2),B(-2,-1)两点.则不等式k1x+b>$\frac{{k}_{2}}{x}$的解集为x>1或-2<x<0.