题目内容
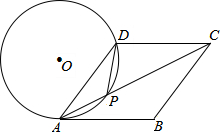 如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD
如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.
(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若AC=8,tan∠DAC=21,求⊙O的半径.
考点:切线的判定,勾股定理,菱形的性质,解直角三角形
专题:证明题
分析:(1)连结OA、OP,设OP与AD交于点H,如图,由PA=PD得PA弧=PD弧,根据垂径定理的推理得OP⊥AD,则∠AHP=90°,再根据菱形的性质得∠DAC=∠BAC,
而∠OAP=∠OPA,则∠OAB=∠OAP+∠BAC=∠OPA+∠DAP=90°,然后根据切线的判定定理即可得到直线AB与⊙O相切;
(2)连结BD交AC于点E,如图,设⊙O的半径为r,根据菱形的性质得AC⊥BD,AE=
AC=4,在Rt△ADE中,利用正切的定义得tan∠DAE=
=
,则DE=2,
再利用勾股定理计算出AD=2
,根据垂径定理由OP⊥AD得AH=DH=
AD=
;在Rt△AHP中,再利用正切的定义得tan∠PAH=
=
,所以HP=
,然后再在Rt△AHO中,根据勾股定理得(
)2+(r-
)2=r2,然后解方程即可.
而∠OAP=∠OPA,则∠OAB=∠OAP+∠BAC=∠OPA+∠DAP=90°,然后根据切线的判定定理即可得到直线AB与⊙O相切;
(2)连结BD交AC于点E,如图,设⊙O的半径为r,根据菱形的性质得AC⊥BD,AE=
| 1 |
| 2 |
| DE |
| AE |
| 1 |
| 2 |
再利用勾股定理计算出AD=2
| 5 |
| 1 |
| 2 |
| 5 |
| PH |
| AH |
| 1 |
| 2 |
| ||
| 2 |
| 5 |
| 1 |
| 2 |
| 5 |
解答:解:(1)直线AB与⊙O相切.理由如下:
连结OA、OP,设OP与AD交于点H,如图,
∵PA=PD,
∴PA弧=PD弧,
∴OP⊥AD,
∴∠AHP=90°
∵四边形ABCD是菱形,
∴∠DAC=∠BAC,
又∵OA=OP,
∴∠OAP=∠OPA,
在Rt△AHP中,∵∠DAP+∠OPA=90°,
∴∠OAB=∠OAP+∠BAC=∠OPA+∠DAP=90°,
即OA⊥AB,
∵点A在⊙O上,
∴直线AB与⊙O相切;
(2)连结BD交AC于点E,如图,设⊙O的半径为r,
∵四边形ABCD是菱形,
∴AC⊥BD,AE=
AC=4,
在Rt△ADE中,tan∠DAE=
=
,
∴DE=2,
∴AD=
=
=2
,
∵OP⊥AD,
∴AH=DH=
AD=
,
在Rt△AHP中,tan∠PAH=
=
,
∴HP=
,
在Rt△AHO中,∵AH2+OH2=OA2,
∴(
)2+(r-
)2=r2,
解得r=
,
即⊙O的半径为
.
连结OA、OP,设OP与AD交于点H,如图,
∵PA=PD,
∴PA弧=PD弧,
∴OP⊥AD,
∴∠AHP=90°
∵四边形ABCD是菱形,
∴∠DAC=∠BAC,
又∵OA=OP,
∴∠OAP=∠OPA,
在Rt△AHP中,∵∠DAP+∠OPA=90°,
∴∠OAB=∠OAP+∠BAC=∠OPA+∠DAP=90°,

即OA⊥AB,
∵点A在⊙O上,
∴直线AB与⊙O相切;
(2)连结BD交AC于点E,如图,设⊙O的半径为r,
∵四边形ABCD是菱形,
∴AC⊥BD,AE=
| 1 |
| 2 |
在Rt△ADE中,tan∠DAE=
| DE |
| AE |
| 1 |
| 2 |
∴DE=2,
∴AD=
| AE2+DE2 |
| 22+42 |
| 5 |
∵OP⊥AD,
∴AH=DH=
| 1 |
| 2 |
| 5 |
在Rt△AHP中,tan∠PAH=
| PH |
| AH |
| 1 |
| 2 |
∴HP=
| ||
| 2 |
在Rt△AHO中,∵AH2+OH2=OA2,
∴(
| 5 |
| 1 |
| 2 |
| 5 |
解得r=
| 5 |
| 4 |
| 5 |
即⊙O的半径为
5
| ||
| 4 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了菱形的性质、勾股定理和解直角三角形.

练习册系列答案
相关题目
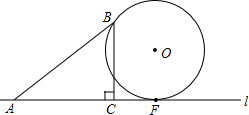 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,边AC在直线l上,点F是直线l上的一个动点,过点B的⊙O与直线l相切于点F.设CF=x,⊙O的半径为y.
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,边AC在直线l上,点F是直线l上的一个动点,过点B的⊙O与直线l相切于点F.设CF=x,⊙O的半径为y.