题目内容
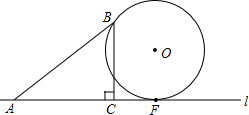 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,边AC在直线l上,点F是直线l上的一个动点,过点B的⊙O与直线l相切于点F.设CF=x,⊙O的半径为y.
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,边AC在直线l上,点F是直线l上的一个动点,过点B的⊙O与直线l相切于点F.设CF=x,⊙O的半径为y.(1)用x的代数式表示y;
(2)点F在运动的过程中,是否存在这样的x,使⊙O与△ABC的两边所在直线同时相切?若存在,求出x的值;若不存在,请说明理由.
考点:圆的综合题
专题:综合题
分析::(1)连接OB,OF,作OD⊥BC于D,如图1,在△ACB,利用勾股定理计算出AB=5,根据切线的性质由过点B的⊙O与直线l相切于点F得到OF⊥l,则可判断四边形OFCD为矩形,所以OD=CF=x,DC=OF=y,则BD=BC-DC=3-y,在Rt△OBD中,利用勾股定理得(3-y)2+x2=y2,变形得到y=
x2+
;
(2)分类讨论:当⊙O与直线AB相切于B点,如图2,连接OB,OF,作OD⊥BC于D,根据切线的性质得OB⊥AB,再利用等角的余角相等得∠ABC=∠DOB,然后根据相似三角形的判定方法得到Rt△ACB∽Rt△BDO,利用相似比得y=
x,由于y=
x2+
,则
x2+
=
x,整理得x2-10x+9=0,解方程得到x1=1,x2=9;
当⊙O与直线BC相切于B点,如图3,连接OB、OF,根据切线长定理易得x=3.
| 1 |
| 6 |
| 3 |
| 2 |
(2)分类讨论:当⊙O与直线AB相切于B点,如图2,连接OB,OF,作OD⊥BC于D,根据切线的性质得OB⊥AB,再利用等角的余角相等得∠ABC=∠DOB,然后根据相似三角形的判定方法得到Rt△ACB∽Rt△BDO,利用相似比得y=
| 5 |
| 3 |
| 1 |
| 6 |
| 3 |
| 2 |
| 1 |
| 6 |
| 3 |
| 2 |
| 5 |
| 3 |
当⊙O与直线BC相切于B点,如图3,连接OB、OF,根据切线长定理易得x=3.
解答:解:(1)连接OB,OF,作OD⊥BC于D,如图1,
在△ABC中,
∵AC=4,BC=3,∠ACB=90°,
∴AB=
=5,
∵过点B的⊙O与直线l相切于点F,
∴OF⊥l,
∴四边形OFCD为矩形,
∴OD=CF=x,DC=OF=y,
∴BD=BC-DC=3-y,
在Rt△OBD中,OB=y,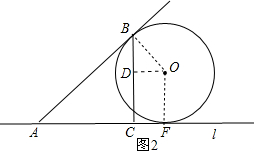
∵BD2+OD2=OB2,
∴(3-y)2+x2=y2,
∴y=
x2+
;
(2)存在.
当⊙O与直线AB相切于B点,如图2,
连接OB,OF,作OD⊥BC于D,
∵AB与⊙O相切于B,
∴OB⊥AB,
∴∠ABO=90°,即∠ABC+∠DBO=90°,
而∠DBO+∠DOB=90°,
∴∠ABC=∠DOB,
∴Rt△ACB∽Rt△BDO,
∴
=
,即
=
,
∴y=
x,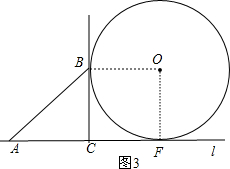
∵y=
x2+
,
∴
x2+
=
x,
整理得x2-10x+9=0,解得x1=1,x2=9,
当⊙O与直线BC相切于B点,如图3,连接OB、OF,
∵BC与⊙O相切于B点,
而⊙O与直线l相切于点F,
∴CB=CF,
∴x=3,
综上所述,满足条件的x的值为1,3,9.

在△ABC中,
∵AC=4,BC=3,∠ACB=90°,
∴AB=
| AC2+BC2 |
∵过点B的⊙O与直线l相切于点F,
∴OF⊥l,
∴四边形OFCD为矩形,
∴OD=CF=x,DC=OF=y,
∴BD=BC-DC=3-y,
在Rt△OBD中,OB=y,

∵BD2+OD2=OB2,
∴(3-y)2+x2=y2,
∴y=
| 1 |
| 6 |
| 3 |
| 2 |
(2)存在.
当⊙O与直线AB相切于B点,如图2,
连接OB,OF,作OD⊥BC于D,
∵AB与⊙O相切于B,
∴OB⊥AB,
∴∠ABO=90°,即∠ABC+∠DBO=90°,
而∠DBO+∠DOB=90°,
∴∠ABC=∠DOB,
∴Rt△ACB∽Rt△BDO,
∴
| AB |
| OB |
| BC |
| OD |
| 5 |
| y |
| 3 |
| x |
∴y=
| 5 |
| 3 |

∵y=
| 1 |
| 6 |
| 3 |
| 2 |
∴
| 1 |
| 6 |
| 3 |
| 2 |
| 5 |
| 3 |
整理得x2-10x+9=0,解得x1=1,x2=9,
当⊙O与直线BC相切于B点,如图3,连接OB、OF,
∵BC与⊙O相切于B点,
而⊙O与直线l相切于点F,
∴CB=CF,
∴x=3,
综上所述,满足条件的x的值为1,3,9.
点评:本题考查了圆的综合题:熟练掌握切线的性质定理、切线长定理;会运用勾股定理和三角形的相似比进行几何计算.

练习册系列答案
相关题目
 如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在C、D之间有一点P.
如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在C、D之间有一点P.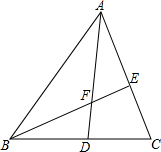 如图,在△ABC中,AD平分∠BAC交BC于D,BE⊥AC于E,交AD于F,求证:∠AFE=
如图,在△ABC中,AD平分∠BAC交BC于D,BE⊥AC于E,交AD于F,求证:∠AFE= (1)在平面直角坐标系中,作出下列各点,A(-3,4),B(-3,-2),O(0,0),并把各点连起来.
(1)在平面直角坐标系中,作出下列各点,A(-3,4),B(-3,-2),O(0,0),并把各点连起来.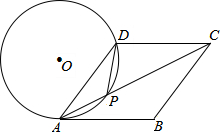 如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD
如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD