题目内容
若a,b,c都是质数,其中a最小,且a+b+c=44,ab+3=c,则ab+c= .
考点:质数与合数
专题:
分析:a,b,c都是质数,且a+b+c=44,那么说明a,b,c中必有一个是偶数(若三个都是奇数的话那和不可能是44),所以a,b,c中必有一个是2,2是最小的质数,其中a最小,那么就能得到 a=2,b+c=42,2b+3=c,解方程组能得出b=13,c=29,再代入计算即可求解.
解答:解:∵a,b,c都是质数,且a+b+c=44,其中a最小,
∴a=2,
依题意有
,
解得
,
∴ab+c=2×13+29=55.
故答案为:55.
∴a=2,
依题意有
|
解得
|
∴ab+c=2×13+29=55.
故答案为:55.
点评:考查了质数与合数,本题关键是由a,b,c都是质数,且a+b+c=44,其中a最小,得出a=2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
不等式组
的解集在数轴上表示为( )
|
A、 |
B、 |
C、 |
D、 |
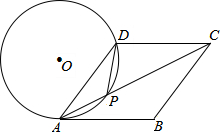 如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD
如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD
 如图所示,?ABCD中,E,G是AD上的两点,F,H是BC上的两点,且AB∥EF∥GH∥DC.则图中的平行四边形共有
如图所示,?ABCD中,E,G是AD上的两点,F,H是BC上的两点,且AB∥EF∥GH∥DC.则图中的平行四边形共有 如图,AB∥CD,∠E=30°,∠B=70°,则∠D=
如图,AB∥CD,∠E=30°,∠B=70°,则∠D=