题目内容
11.一个四边形的四个内角的度数之比是3:3:2:1,求这个四边形的最小内角是40°.分析 设四边形4个内角的度数分别是3x,3x,2x,x,所以3x+3x+2x+x=360°,解得x=20°,则可以求得最小内角的度数.
解答 解:设四边形4个内角的度数分别是3x,3x,2x,x,
所以3x+3x+2x+x=360°,
解得x=40°.
则最小内角为40×1=20°.
故答案为:40°.
点评 本题主要考查了四边形的内角和是360度的具体运用.

练习册系列答案
相关题目
2.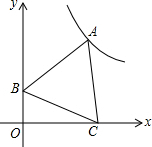 如图,点A是反比例函数y=$\frac{12\sqrt{3}}{x}$(x>0)图象上一点,点C是x正半轴上一点,点B的坐标为(0,$\sqrt{3}$),当△ABC是等边三角形时,点A的坐标为( )
如图,点A是反比例函数y=$\frac{12\sqrt{3}}{x}$(x>0)图象上一点,点C是x正半轴上一点,点B的坐标为(0,$\sqrt{3}$),当△ABC是等边三角形时,点A的坐标为( )
 如图,点A是反比例函数y=$\frac{12\sqrt{3}}{x}$(x>0)图象上一点,点C是x正半轴上一点,点B的坐标为(0,$\sqrt{3}$),当△ABC是等边三角形时,点A的坐标为( )
如图,点A是反比例函数y=$\frac{12\sqrt{3}}{x}$(x>0)图象上一点,点C是x正半轴上一点,点B的坐标为(0,$\sqrt{3}$),当△ABC是等边三角形时,点A的坐标为( )| A. | (3$\sqrt{3}$,4) | B. | (4,3$\sqrt{3}$) | C. | (4$\sqrt{3}$,3) | D. | (3,4$\sqrt{3}$) |
6.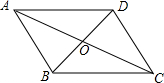 如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )
如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )
 如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )
如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )| A. | DC=BC | B. | AC⊥BD | C. | AB=BD | D. | ∠ADB=∠CDB |
16.若式子$\frac{\sqrt{x-1}}{x+2}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥1且x≠0 | B. | x>1 且x≠-2 | C. | x≥1 | D. | x≥1 且x≠-2 |
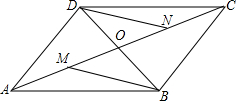 如图所示,?ABCD的对角线AC,BD相交于O,M是AO的中点,N是CO的中点,则BM与DN有什么关系?证明你的结论.
如图所示,?ABCD的对角线AC,BD相交于O,M是AO的中点,N是CO的中点,则BM与DN有什么关系?证明你的结论.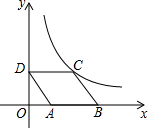 如图,?ABCD放置在平面直角坐标系中,已知点A(2,0),B(6,0),D(0,3).反比例函数的图象经过点C,则反比例函数的解析式是y=$\frac{12}{x}$(x≠0).
如图,?ABCD放置在平面直角坐标系中,已知点A(2,0),B(6,0),D(0,3).反比例函数的图象经过点C,则反比例函数的解析式是y=$\frac{12}{x}$(x≠0).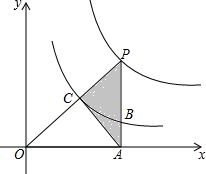 如图所示,已知点P为反比例函数y=$\frac{4}{x}$(x>0)图象上的一点,且PA⊥x轴于点A,PA,PO分别交于反比例函数y=$\frac{1}{x}$图象于B,C两点,则△PAC的面积为( )
如图所示,已知点P为反比例函数y=$\frac{4}{x}$(x>0)图象上的一点,且PA⊥x轴于点A,PA,PO分别交于反比例函数y=$\frac{1}{x}$图象于B,C两点,则△PAC的面积为( )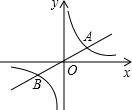 如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为4.
如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为4.