题目内容
已知a,b,c分别是△ABC中∠A,∠B,∠C的对边,a,b,c满足(2b)2=4(c+a)(c-a),且有5a-3c=0.求sinA的值.
考点:解直角三角形,勾股定理的逆定理
专题:计算题
分析:已知第一个等式变形,利用勾股定理的逆定理得到三角形ABC为直角三角形,且∠C为直角,利用锐角三角函数定义求出sinA的值即可.
解答:解:已知等式变形得:4b2=4c2-4a2,即a2+b2=c2,
∴△ABC为直角三角形,即∠C=90°,
∵5a-3c=0,即
=
,
∴sinA=
=
.
∴△ABC为直角三角形,即∠C=90°,
∵5a-3c=0,即
| a |
| c |
| 3 |
| 5 |
∴sinA=
| a |
| c |
| 3 |
| 5 |
点评:此题考查了解直角三角形,锐角三角函数定义,以及勾股定理的逆定理,熟练掌握勾股定理的逆定理是解本题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
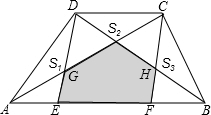 如图所示,AB∥DC,DE∥CF,已知△ADG的面积为S1,△CDO的面积为S2,△BCH的面积为S3,若S1=19,S2=18,S3=22.8,则五边形EGOHF的面积为
如图所示,AB∥DC,DE∥CF,已知△ADG的面积为S1,△CDO的面积为S2,△BCH的面积为S3,若S1=19,S2=18,S3=22.8,则五边形EGOHF的面积为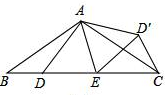 如图,在△ABC中,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD′,连结D′E,DE′=DE.
如图,在△ABC中,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD′,连结D′E,DE′=DE. 如图,各小方格的边长为1,△ABC的各个顶点都在格点上,求AB边上的高.
如图,各小方格的边长为1,△ABC的各个顶点都在格点上,求AB边上的高.