题目内容
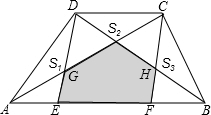如图所示，AB∥DC，DE∥CF，已知△ADG的面积为S1，△CDO的面积为S2，△BCH的面积为S3，若S1=19，S2=18，S3=22.8，则五边形EGOHF的面积为考点：面积及等积变换
专题：
分析：易证四边形CDEF是平行四边形，设DC与AB之间的距离为h，易得S?CDEF=S△ADC+S△BDC，由此可推出S五边形EGOHF=S1+S2+S3，问题得以解决．
解答：解：∵AB∥DC，DE∥CF，
∴四边形CDEF是平行四边形．
设DC与AB之间的距离为h，
则S?CDEF=DC•h，S△ADC=S△BDC=
DC•h，
∴S?CDEF=S△ADC+S△BDC，
∴S2+S△DOG+S△COH+S五边形EGOHF=S1+S△DOG+S2+S3+S△COH+S2，
∴S五边形EGOHF=S1+S2+S3．
∵S1=19，S2=18，S3=22.8，
∴S五边形EGOHF=19+18+22.8=59.8．
故答案为：59.8．
∴四边形CDEF是平行四边形．
设DC与AB之间的距离为h，
则S?CDEF=DC•h，S△ADC=S△BDC=
| 1 |
| 2 |
∴S?CDEF=S△ADC+S△BDC，
∴S2+S△DOG+S△COH+S五边形EGOHF=S1+S△DOG+S2+S3+S△COH+S2，
∴S五边形EGOHF=S1+S2+S3．
∵S1=19，S2=18，S3=22.8，
∴S五边形EGOHF=19+18+22.8=59.8．
故答案为：59.8．
点评：本题主要考查了平行四边形的判定、平行四边形及三角形的面积公式、等积变换等知识，推出S?CDEF=S△ADC+S△BDC是解决本题的关键．
练习册系列答案
相关题目