题目内容
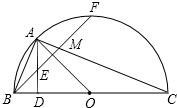 如图,已知BC为半圆O的直径,
如图,已知BC为半圆O的直径, |
| AB |
 |
| AF |
| 5 |
| 4 |
| ED |
| BD |
| 3 |
| 4 |
考点:圆周角定理,等边三角形的判定与性质,勾股定理
专题:
分析:由条件可得出∠EBA=∠EAB,得到AE=BE=EM,在Rt△BDE中可求得BE和BD,从而可求得AD,且容易证明△ABD∽△CAD,可得到AD2=BD•CD,可求得CD.
解答:解:
∵
=
,
∴∠ACB=∠EBA,
∵AB为直径,AD⊥BC,
∴∠ACB+∠DAC=∠BAE+∠DAC=90°,
∴∠BAE=∠ACB,
∴∠EBA=∠EAB,
∵∠BAE+∠EAM=∠EMA+∠ABE,
∴∠EAM=∠EMA,
∴AE=BE=EM=
,
∵
=
,
设ED=3x,BD=4x,在Rt△BDE中由勾股定理可得ED2+BD2=BE2,
即(3x)2+(4x)2=(
)2,解得x=
或-
(舍去),
∴DE=
,BD=1,AD=
+
=2,
在△ABD和△CAD中,∠ADB=∠CDA,∠BAD=∠ACD,
∴△ABD∽△CAD,
∴
=
,即
=
,
∴CD=4.
∵
 |
| AB |
 |
| AF |
∴∠ACB=∠EBA,
∵AB为直径,AD⊥BC,
∴∠ACB+∠DAC=∠BAE+∠DAC=90°,
∴∠BAE=∠ACB,
∴∠EBA=∠EAB,
∵∠BAE+∠EAM=∠EMA+∠ABE,
∴∠EAM=∠EMA,
∴AE=BE=EM=
| 5 |
| 4 |
∵
| ED |
| BD |
| 3 |
| 4 |
设ED=3x,BD=4x,在Rt△BDE中由勾股定理可得ED2+BD2=BE2,
即(3x)2+(4x)2=(
| 5 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
∴DE=
| 3 |
| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
在△ABD和△CAD中,∠ADB=∠CDA,∠BAD=∠ACD,
∴△ABD∽△CAD,
∴
| AD |
| CD |
| BD |
| AD |
| 2 |
| CD |
| 1 |
| 2 |
∴CD=4.
点评:本题主要考查圆周角定理和等腰三角形的判定和性质、相似三角形的判定和性质,先求得AE=BE=EM是解题的关键,注意方程思想的应用.

练习册系列答案
相关题目
若函数y=
与y=kx的图象的一个交点为(-2,3),则它们图象的另一个交点为( )
| k |
| x |
| A、(-3,2) |
| B、(2,-3) |
| C、(-2,-3) |
| D、(-3,-2) |
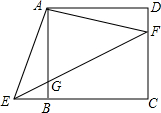 如图,在正方形ABCD中,F是CD上的一点,AE⊥AF,E是BC的延长线上一点,EF交AB于点G.
如图,在正方形ABCD中,F是CD上的一点,AE⊥AF,E是BC的延长线上一点,EF交AB于点G. 如图所示,点C是线段AB上的一点,点M是线段AC的中点,点N是线段BC的中点.
如图所示,点C是线段AB上的一点,点M是线段AC的中点,点N是线段BC的中点. 如图,D、E分别是△ABC的边AC、AB上的点.AE=1.5,AC=2,BC=3,且
如图,D、E分别是△ABC的边AC、AB上的点.AE=1.5,AC=2,BC=3,且 如图,在正八边形ABCDEFGH中,AC、GC是两条对角线,则∠ACG=
如图,在正八边形ABCDEFGH中,AC、GC是两条对角线,则∠ACG=