题目内容
若函数y=mx2-4x+3的图象与x轴只有一个公共点,则m的取值为 .
考点:抛物线与x轴的交点
专题:
分析:根据函数y=mx2-4x+3的图象与x轴只有一个公共点,函数y=mx2-4x+3为一次函数或二次函数,若为一次函数则m=0,若为二次函数则(-4)2-4×3m=0,从而求得m的值.
解答:解:分两种情况:
①若y=mx2-4x+3为一次函数,则m=0;
②若y=mx2-4x+3为二次函数,则(-4)2-4×3m=0,
∴16-12m=0,解得m=
,
故答案为:0或
.
①若y=mx2-4x+3为一次函数,则m=0;
②若y=mx2-4x+3为二次函数,则(-4)2-4×3m=0,
∴16-12m=0,解得m=
| 4 |
| 3 |
故答案为:0或
| 4 |
| 3 |
点评:本题考查了抛物线与x轴的交点问题,当不确定是什么函数时,要分类讨论.

练习册系列答案
相关题目
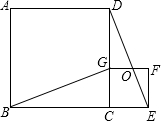 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③| DG |
| GC |
| GO |
| CE |
| A、①②③ | B、②③④ |
| C、①②④ | D、①②③④ |
一次函数y=kx-k(k<0)的图象大致是( )
A、 |
B、 |
C、 |
D、 |
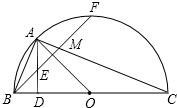 如图,已知BC为半圆O的直径,
如图,已知BC为半圆O的直径,
 如图,在Rt△ABC中,∠C=90°,AD是中线,若AC=3cm,BC=4cm,则△ABD的面积是
如图,在Rt△ABC中,∠C=90°,AD是中线,若AC=3cm,BC=4cm,则△ABD的面积是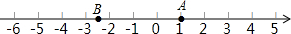 根据下面给出的数轴,解答下面的问题:
根据下面给出的数轴,解答下面的问题: 如图,正五边形ABCDE内接于圆O,对角线AC、BD交于点P,则∠APD=
如图,正五边形ABCDE内接于圆O,对角线AC、BD交于点P,则∠APD=