题目内容
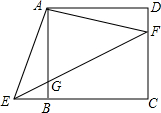 如图,在正方形ABCD中,F是CD上的一点,AE⊥AF,E是BC的延长线上一点,EF交AB于点G.
如图,在正方形ABCD中,F是CD上的一点,AE⊥AF,E是BC的延长线上一点,EF交AB于点G.(1)求证:DF•FC=BG•EC;
(2)当tan∠DAF=
| 1 |
| 3 |
考点:相似三角形的判定与性质,正方形的性质
专题:
分析:(1)由正方形的性质,结合条件可证明△ABE≌△ADF,可得BE=DF,又△BEG∽△CEF,可得BG:CF=BE:EC,可得BE•FC=BG•EC,可得到结论;
(2)由(1)可知AE=AF,则△AEF的面积为10可得AF2=20,求得AF,又tan∠DAF=
,可得到
=
,结合勾股定理可求得AD.
(2)由(1)可知AE=AF,则△AEF的面积为10可得AF2=20,求得AF,又tan∠DAF=
| 1 |
| 3 |
| DF |
| AD |
| 1 |
| 3 |
解答:(1)证明:∵四边形ABCD为正方形,
∴AB=AD,∠ABE=∠ADF=∠BAD=90°,
∵AE⊥AF,
∴∠EAB+∠BAF=∠BAF+∠DAF=90°,
∴∠BAE=∠DAF,
在△ABE和△ADF中
∴△ABE≌△ADF(ASA),
∴BE=DF,
∵BG∥FC,
∴△BEG∽△CEF,
∴BG:CF=BE:EC,即BE•FC=BG•EC,
∴DF•FC=BG•EC;
(2)解:由(1)可知△ABE≌△ADF,
∴AE=AF,且AE⊥AF,
∴S△AEF=
AE•AF=
AF2=10,
解得AF=2
,
∵tan∠DAF=
=
,
设DF=x,则AD=3x,在Rt△ADF中,由勾股定理可得DF2+AD2=AF2,
即x2+(3x)2=20,解得x=
或-
(舍去),
∴AD=3
,
即正方形的边长为3
.
∴AB=AD,∠ABE=∠ADF=∠BAD=90°,
∵AE⊥AF,
∴∠EAB+∠BAF=∠BAF+∠DAF=90°,
∴∠BAE=∠DAF,
在△ABE和△ADF中
|
∴△ABE≌△ADF(ASA),
∴BE=DF,
∵BG∥FC,
∴△BEG∽△CEF,
∴BG:CF=BE:EC,即BE•FC=BG•EC,
∴DF•FC=BG•EC;
(2)解:由(1)可知△ABE≌△ADF,
∴AE=AF,且AE⊥AF,
∴S△AEF=
| 1 |
| 2 |
| 1 |
| 2 |
解得AF=2
| 5 |
∵tan∠DAF=
| DF |
| AD |
| 1 |
| 3 |
设DF=x,则AD=3x,在Rt△ADF中,由勾股定理可得DF2+AD2=AF2,
即x2+(3x)2=20,解得x=
| 2 |
| 2 |
∴AD=3
| 2 |
即正方形的边长为3
| 2 |
点评:本题主要考查相似三角形的判定和性质及全等三角形的判定和性质,在(1)中证得BE=DF是解题的关键,在第(2)问求出AF是解题的关键,注意方程思想的应用.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
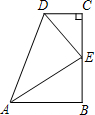 如图,∠B=∠C=90°,E是BC的中点,DE平分线∠ADC,则下列结论不正确是( )
如图,∠B=∠C=90°,E是BC的中点,DE平分线∠ADC,则下列结论不正确是( )| A、AE平分∠DAE |
| B、AB∥CD |
| C、△EBA≌△DCE |
| D、AB+CD=AD |
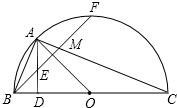 如图,已知BC为半圆O的直径,
如图,已知BC为半圆O的直径,
 如图,正五边形ABCDE内接于圆O,对角线AC、BD交于点P,则∠APD=
如图,正五边形ABCDE内接于圆O,对角线AC、BD交于点P,则∠APD=