题目内容
 如图,在正八边形ABCDEFGH中,AC、GC是两条对角线,则∠ACG=
如图,在正八边形ABCDEFGH中,AC、GC是两条对角线,则∠ACG=考点:正多边形和圆
专题:
分析:如图,首先证明
=
=
圆周长,然后求出
的度数=
×360°=90°,问题即可解决.
 |
| AH |
 |
| GH |
| 1 |
| 8 |
 |
| AHG |
| 2 |
| 8 |
解答: 解:设正八边形ABCDEFGH的外接圆为⊙O;
解:设正八边形ABCDEFGH的外接圆为⊙O;
∵正八边形ABCDEFGH的各边相等,
∴
=
=
圆周长,
∴
的度数=
×360°=90°,
∴圆周角∠ACG=
×90°=45°.
故答案为45°.
 解:设正八边形ABCDEFGH的外接圆为⊙O;
解:设正八边形ABCDEFGH的外接圆为⊙O;∵正八边形ABCDEFGH的各边相等,
∴
 |
| AH |
 |
| GH |
| 1 |
| 8 |
∴
 |
| AHG |
| 2 |
| 8 |
∴圆周角∠ACG=
| 1 |
| 2 |
故答案为45°.
点评:该题以正多边形及其外接圆为载体,以正多边形的性质及其应用的考查为核心构造而成;对分析问题解决问题能力提出了一定的要求.

练习册系列答案
相关题目
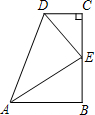 如图,∠B=∠C=90°,E是BC的中点,DE平分线∠ADC,则下列结论不正确是( )
如图,∠B=∠C=90°,E是BC的中点,DE平分线∠ADC,则下列结论不正确是( )| A、AE平分∠DAE |
| B、AB∥CD |
| C、△EBA≌△DCE |
| D、AB+CD=AD |
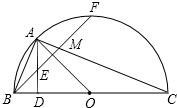 如图,已知BC为半圆O的直径,
如图,已知BC为半圆O的直径,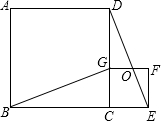 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③ 如图,在Rt△ABC中,∠C=90°,AD是中线,若AC=3cm,BC=4cm,则△ABD的面积是
如图,在Rt△ABC中,∠C=90°,AD是中线,若AC=3cm,BC=4cm,则△ABD的面积是 如图,正五边形ABCDE内接于圆O,对角线AC、BD交于点P,则∠APD=
如图,正五边形ABCDE内接于圆O,对角线AC、BD交于点P,则∠APD=