题目内容
 如图,抛物线y=-x2+bx+c经过A(-1,0)、C(0,4)两点,与x轴的另一交点是B.
如图,抛物线y=-x2+bx+c经过A(-1,0)、C(0,4)两点,与x轴的另一交点是B.(1)求抛物线的解析式;
(2)若点D(a,a+1)在第一象限的抛物线上,求点D关于直线BC的对称点D′的坐标;
(3)在(2)的条件下,过点D作DE⊥BC于点E,反比例函数y=
| k |
| x |
| 3 |
| 15 |
| m |
考点:二次函数综合题
专题:
分析:(1)直接利用待定系数法求出抛物线解析式即可;
(2)首先求出D点坐标,进而求出∠DCB=45°=∠BCD,则点D′在y轴上,且CD=CD′=3,即可得出D′点坐标;
(3)首先利用D,D′点坐标得出E点坐标,即可得出反比例函数解析式,进而得出4n-
的值.
(2)首先求出D点坐标,进而求出∠DCB=45°=∠BCD,则点D′在y轴上,且CD=CD′=3,即可得出D′点坐标;
(3)首先利用D,D′点坐标得出E点坐标,即可得出反比例函数解析式,进而得出4n-
| 15 |
| m |
解答: 解:(1)∵抛物线y=-x2+bx+c经过A(-1,0)、C(0,4)两点,
解:(1)∵抛物线y=-x2+bx+c经过A(-1,0)、C(0,4)两点,
∴
,
解得:
,
∴抛物线的解析式为:y=-x2+3x+4;
(2)∵y=-x2+3x+4,B点在x轴上,
∴点B(0,4),OB=4,
∵点D(a,a+1)在第一象限的抛物线上,
∴a+1=-a2+3a+4,
解得:a1=3,a2=-1,
∵点D(a,a+1)在第一象限,
∴a2=-1不合题意舍去,
∴a=3,
∴点D(3,4),
∵C(0,4),
∴CD∥x轴,CD=3,
∵OC=4,OB=4,
∴∠OCB=45°=∠BCD,
∴点D′在y轴上,且CD=CD′=3,
∴点D′(0,1);
(3)∵点D(3,4),点D′(0,1),
∴点E(
,
),
∴反比例函数解析式为:y=
,
∵点F(m,n-
)在反比例函数y=
图象上,
∴m≠0,
∴m(n-
)=
,
∴4m(n-
)=15,
∵m≠0,
∴4n-4
=
,
∴4n-
=4
.
 解:(1)∵抛物线y=-x2+bx+c经过A(-1,0)、C(0,4)两点,
解:(1)∵抛物线y=-x2+bx+c经过A(-1,0)、C(0,4)两点,∴
|
解得:
|
∴抛物线的解析式为:y=-x2+3x+4;
(2)∵y=-x2+3x+4,B点在x轴上,
∴点B(0,4),OB=4,
∵点D(a,a+1)在第一象限的抛物线上,
∴a+1=-a2+3a+4,
解得:a1=3,a2=-1,
∵点D(a,a+1)在第一象限,
∴a2=-1不合题意舍去,
∴a=3,
∴点D(3,4),
∵C(0,4),
∴CD∥x轴,CD=3,
∵OC=4,OB=4,
∴∠OCB=45°=∠BCD,
∴点D′在y轴上,且CD=CD′=3,
∴点D′(0,1);
(3)∵点D(3,4),点D′(0,1),
∴点E(
| 3 |
| 2 |
| 5 |
| 2 |
∴反比例函数解析式为:y=
| 15 |
| 4x |
∵点F(m,n-
| 3 |
| 15 |
| 4x |
∴m≠0,
∴m(n-
| 3 |
| 15 |
| 4 |
∴4m(n-
| 3 |
∵m≠0,
∴4n-4
| 3 |
| 15 |
| m |
∴4n-
| 15 |
| m |
| 3 |
点评:此题主要考查了二次函数综合以及等腰直角三角形的性质和图象上点的坐标性质等知识,利用数形结合得出点D′位置是解题关键.

练习册系列答案
相关题目
某校为了解学校学生的视力情况,从全校学生中随机抽取了200个学生进行检查.则下列说法错误的是( )
| A、本次的调查方式是抽样调查 |
| B、该校每一个学生是本次调查的个体 |
| C、本次调查的样本容量是200 |
| D、被抽取的这200个学生的视力情况是本次调查的样本 |
张大爷承包了一个鱼塘养鱼,在鱼成熟上市以前,为了解鱼塘内鱼的条数,他先捞上100条鱼,做上记号后放回鱼塘.第二天又捞上100条鱼,发现做了记号的鱼有2条,则鱼塘内鱼的数量(单位:条)大约有( )
| A、2000 | B、5000 |
| C、8000 | D、20000 |
 如图,在?ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.
如图,在?ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.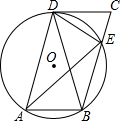 如图,在?ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.
如图,在?ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.