题目内容
17. 如图,四边形ABCD是平行四边形,DB⊥AD,AD=8cm,BD=12cm,求BC,AC的长.
如图,四边形ABCD是平行四边形,DB⊥AD,AD=8cm,BD=12cm,求BC,AC的长.
分析 在平行四边形中,可由对边分别相等得出BC的长,再在Rt△ABD中,由勾股定理得出线段OA的长,进而可求解AC的长.
解答 解:∵四边形ABCD是平行四边形,
∴BC=AD=8cm,OA=OC,OB=OD=$\frac{1}{2}$BD=6cm,
∵BD⊥AD,
∴∠ADO=90°,
∴OA=$\sqrt{A{D}^{2}+O{D}^{2}}$=10cm,
∴AC=2OA=20cm.
点评 本题主要考查平行四边形的性质及勾股定理的运用,熟练掌握平行四边形的性质和勾股定理是关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
7.化简:-$\sqrt{(1-sin52°)^{2}}$-$\sqrt{(1-tan52°)^{2}}$的结果是( )
| A. | tan52°-sin52° | B. | sin52°-tan52° | C. | 2-sin52°-tan52° | D. | -sin52°-tan52° |
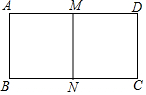 如图,矩形ABCD中,AB=4,M、N分别是AD、BC的中点,MN∥AB,若矩形DMNC与矩形ABCD相似,则AD的长为4$\sqrt{2}$.
如图,矩形ABCD中,AB=4,M、N分别是AD、BC的中点,MN∥AB,若矩形DMNC与矩形ABCD相似,则AD的长为4$\sqrt{2}$.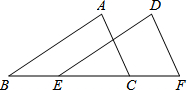 如图,已知△ABC≌△DEF,点B,E,C,F在同一条直线上,若BC=5,BE=2,则BF=7.
如图,已知△ABC≌△DEF,点B,E,C,F在同一条直线上,若BC=5,BE=2,则BF=7. 如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若BE:BC=1:4,则S△BDE:S△ACD的比为1:12.
如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若BE:BC=1:4,则S△BDE:S△ACD的比为1:12.