题目内容
13.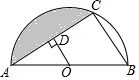 如图,O为半圆的圆心,直径AB=12,C是半圆上一点,OD⊥AC于点D,OD=3.
如图,O为半圆的圆心,直径AB=12,C是半圆上一点,OD⊥AC于点D,OD=3.(1)求AC的长;
(2)求图中阴影部分的面积.
分析 (1)根据垂径定理可知AD=DC,由OA=OB,推出BC=2OD=6,Z在Rt△ACB中,利用勾股定理求出AC.
(2)首先证明△OBC设等边三角形,推出∠AOC=120°,根据S阴=S扇形OAC-S△AOC计算即可.
解答 解:(1)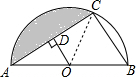 ∵OD⊥AC,
∵OD⊥AC,
∴AD=DC,∵AO=OB,
∴BC=2OD=6,
∵AB是直径,
∴∠ACB=90°,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$.
(2)连接OC,∵OC=OB=BC=6,
∴∠BOC=60°,
∴∠AOC=120°,
∴S阴=S扇形OAC-S△AOC=$\frac{120•π•{6}^{2}}{360}$-$\frac{1}{2}$•6$\sqrt{3}$•3=12π-9$\sqrt{3}$.
点评 本题考查扇形的面积公式、垂径定理、勾股定理.三角形的中位线定理等知识,解题的关键是学会添加常用辅助线,学会用方法求阴影部分面积,属于中考常考题型.

练习册系列答案
相关题目
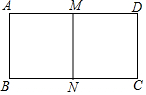 如图,矩形ABCD中,AB=4,M、N分别是AD、BC的中点,MN∥AB,若矩形DMNC与矩形ABCD相似,则AD的长为4$\sqrt{2}$.
如图,矩形ABCD中,AB=4,M、N分别是AD、BC的中点,MN∥AB,若矩形DMNC与矩形ABCD相似,则AD的长为4$\sqrt{2}$. 如图,点O是直线AB上一点,OC是一条射线,且∠AOC=32°,若过点O作射线OD,使OD⊥OC,则∠BOD的度数为58°或122°.
如图,点O是直线AB上一点,OC是一条射线,且∠AOC=32°,若过点O作射线OD,使OD⊥OC,则∠BOD的度数为58°或122°.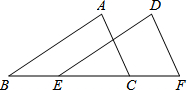 如图,已知△ABC≌△DEF,点B,E,C,F在同一条直线上,若BC=5,BE=2,则BF=7.
如图,已知△ABC≌△DEF,点B,E,C,F在同一条直线上,若BC=5,BE=2,则BF=7.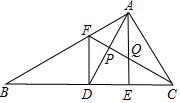 如图,D为△ABC中边BC中点,E为CD上一点,将△ACE沿AE折叠时C与D重合,F为AB上一点,FB=FC,FC与AD、AE分别交于P、Q点,下列结论
如图,D为△ABC中边BC中点,E为CD上一点,将△ACE沿AE折叠时C与D重合,F为AB上一点,FB=FC,FC与AD、AE分别交于P、Q点,下列结论