题目内容
某通讯器材商场,计划从一厂家购进若干部新型手机以满足市场需求,已知该厂家生产三种不同型号的手机,出厂价分别是甲种型号手机1800元/部,乙种型号手机600元/部,丙种型号手机1200元/部.商场在经销中,甲种型号手机可赚200元/部,乙种型号手机可赚100元/部,丙种型号手机可赚120元/部.
(1)若商场用6万元同时购进两种不同型号的手机共40部,并恰好将钱用完,请你通过计算分析进货方案;
(2)在(1)的条件下,求盈利最多的进货方案;
(3)若该商场同时购进三种手机,且购进甲,丙两种手机用了3.9万元,预计可获得5000元利润,问这次经销商共有几种可能的方案?最低成本(进货额)多少元?
(1)若商场用6万元同时购进两种不同型号的手机共40部,并恰好将钱用完,请你通过计算分析进货方案;
(2)在(1)的条件下,求盈利最多的进货方案;
(3)若该商场同时购进三种手机,且购进甲,丙两种手机用了3.9万元,预计可获得5000元利润,问这次经销商共有几种可能的方案?最低成本(进货额)多少元?
考点:二元一次方程的应用
专题:
分析:(1)商场用6万元同时购进两种不同型号的手机有三类不同的方案:①购进甲乙两种,②乙丙两种,③购进甲丙两种.然后根据购进的两种手机的部数和=40,购机两种手机用的总费用=6万元,这两个等量关系来列出方程组,解方程组即可.
(2)根据(1)得出的方案,计算出各方案的盈利额,然后比较哪种盈利较多;
(3)根据题意列出方程得出z=
,y=11-
x的关系式讨论即可得出方案,再选择成本最低的方案.
(2)根据(1)得出的方案,计算出各方案的盈利额,然后比较哪种盈利较多;
(3)根据题意列出方程得出z=
| 65-3x |
| 2 |
| 1 |
| 5 |
解答:解:设甲种型号手机x部,乙种手机y部,丙种手机z部.
(1)根据题意得:①
.
解得
.
②
.
解得
.
③
.
解得
(不合题意,舍去).
答:有两种购买方案:甲种型号手机30部,乙种手机10部;或甲种型号手机20部,丙种手机20部;
(2)方案一盈利:200×30+100×10=7000(元)
方案二盈利:200×20+120×20=6400(元)
所以购买甲种型号手机30部,乙种手机10部所获盈利较大;
(3)由题意建立方程组为:
,
由①得:z=
,
由②×10-①得:y=11-
x,
∵11-
x≥0且x、y、z都是自然数,
∴x可以是15,5,
∴这次经销商共有2种可能的方案,
当x=15时,y=8,z=10,
1800x+600y+1200z=1800×15+600×8+1200×10=43800(元).
当x=5时,y=10,z=25,
1800x+600y+1200z=1800×5+600×10+1200×25=45000(元).
答:这次经销商共有2种可能的方案,最低成本(进货额)43800元.
(1)根据题意得:①
|
解得
|
②
|
解得
|
③
|
解得
|
答:有两种购买方案:甲种型号手机30部,乙种手机10部;或甲种型号手机20部,丙种手机20部;
(2)方案一盈利:200×30+100×10=7000(元)
方案二盈利:200×20+120×20=6400(元)
所以购买甲种型号手机30部,乙种手机10部所获盈利较大;
(3)由题意建立方程组为:
|
由①得:z=
| 65-3x |
| 2 |
由②×10-①得:y=11-
| 1 |
| 5 |
∵11-
| 1 |
| 5 |
∴x可以是15,5,
∴这次经销商共有2种可能的方案,
当x=15时,y=8,z=10,
1800x+600y+1200z=1800×15+600×8+1200×10=43800(元).
当x=5时,y=10,z=25,
1800x+600y+1200z=1800×5+600×10+1200×25=45000(元).
答:这次经销商共有2种可能的方案,最低成本(进货额)43800元.
点评:此题比较复杂,根据已知条件首先要分类讨论,然后在可能的情况下分别列出方程组,解方程组根据解的情况就可以确定购买方案.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
如果点P(m,3)与点Q(-5,n)关于y轴对称,则m,n的值分别为( )
| A、m=-5,n=3 |
| B、m=5,n=3 |
| C、m=5,n=-3 |
| D、m=-3,n=5 |

 如图,四边形ABCD是直角梯形,AD∥BC,∠B=90°,AB=8cm,AD=24cm.BC=26cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动.设运动的时间为t(秒).
如图,四边形ABCD是直角梯形,AD∥BC,∠B=90°,AB=8cm,AD=24cm.BC=26cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动.设运动的时间为t(秒). 如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,记四边形A1ABB1的面积为S1;再分别取A1C、B1C的中点A2、B2,记四边形A2A1B1B2的面积为S2;再分别取A2C、B2C的中点A3、B3,依次取下去…
如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,记四边形A1ABB1的面积为S1;再分别取A1C、B1C的中点A2、B2,记四边形A2A1B1B2的面积为S2;再分别取A2C、B2C的中点A3、B3,依次取下去… 夏天到了,欣欣服装店老板用4500元购进一批卡通团T桖衫,由于深受顾客喜爱,很快售完,老板又用5000元购进第二批该款式T恤杉,所购数量与第一批相同,但每件进价比第一批多了10元.
夏天到了,欣欣服装店老板用4500元购进一批卡通团T桖衫,由于深受顾客喜爱,很快售完,老板又用5000元购进第二批该款式T恤杉,所购数量与第一批相同,但每件进价比第一批多了10元.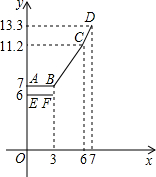 为缓解油价上涨给出租车行业带来的成本压力,某市自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
为缓解油价上涨给出租车行业带来的成本压力,某市自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)