题目内容
(1)解不等式组
,并把解集在数轴上表示出来.
(2)先化简,再求代数式
÷(a-
)的值,其中a=3tan30°+1,b=
cos45°.
|
(2)先化简,再求代数式
| a-b |
| a |
| 2ab-b2 |
| a |
| 2 |
考点:解一元一次不等式组,分式的化简求值,特殊角的三角函数值
专题:计算题
分析:(1)先解两个不等式,再把解集画在数轴上,得出解集即可;
(2)先化简a,b,再化简代数式,再代入数据即可.
(2)先化简a,b,再化简代数式,再代入数据即可.
解答:解:(1)解第一个不等式得:x≤1
解第二个不等式得:x>-2
所以不等式组的解集为:-2<x≤1

(2)原式=
÷
=
•
=
,
∵a=3tan30°+1=
+1,
b=
cos45°=1,
∴把a,b的值代入上式得:原式=
=
.
解第二个不等式得:x>-2
所以不等式组的解集为:-2<x≤1

(2)原式=
| a-b |
| a |
| a2-2ab+b2 |
| a |
| a-b |
| a |
| a |
| (a-b)2 |
| 1 |
| a-b |
∵a=3tan30°+1=
| 3 |
b=
| 2 |
∴把a,b的值代入上式得:原式=
| 1 | ||
|
| ||
| 3 |
点评:本题考查了解一元一次不等式组、分式的化简求值以及特殊角的三角函数值,是基础知识要熟练掌握.

练习册系列答案
相关题目
若(x2+x+1)6=a12x12+a11x11+a10x10+…+a1x+a0,则a11+a9+a7+a5+a3+a1=( )
| A、364 | B、365 |
| C、730 | D、728 |
 样本,绘制成绩统计图如图所示,请结合统计图回答下列问题.
样本,绘制成绩统计图如图所示,请结合统计图回答下列问题.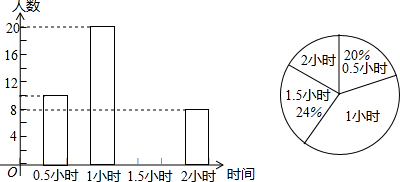
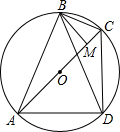 如图:已知点A、B、C、D顺次在圆O上,AB=BD,BM⊥AC,垂足为M.证明:AM=DC+CM.(阿基米德折弦定理)
如图:已知点A、B、C、D顺次在圆O上,AB=BD,BM⊥AC,垂足为M.证明:AM=DC+CM.(阿基米德折弦定理)