题目内容
17.如图1,点B在线段AC上的黄金分割点,且AB>BC.(1)设AC=2,
①求AB的长;
填空:设AB=x,则BC=2-x
∵点B在线段AC上的黄金分割点,且AB>BC,
∴$\frac{AB}{AC}$=$\frac{BC}{AB}$,可列方程为$\frac{x}{2}$=$\frac{2-x}{x}$,
解得方程的根为x1=-1+$\sqrt{5}$,x2=-1-$\sqrt{5}$,于是,AB的长为-1+$\sqrt{5}$.
②在线段AC(如图1)上利用三角板和圆规画出点B的位置(保留作图痕迹,不写作法);
(2)若m、n为正实数,t是关于x的方程x2+2mx=n2的一正实数根,
①求证:(t+m)2=m2+n2;
②若两条线段的长分别为m、n(如图2),请画出一条长为t的线段(保留作图痕迹,不写作法).

分析 (1)若点B在线段AC上的黄金分割点,且AB>BC,则$\frac{AB}{AC}$=$\frac{BC}{AB}$,设AB=x,则BC=2-x代入求值即可.
(2)①利用勾股定理画出$\sqrt{5}$,再在长为$\sqrt{5}$的线段上截取长为1的线段,剩余部分就是$\sqrt{5}-1$.
②根据配方法解该方程的根即可,作图与①雷同.
解答 解:(1)①设AB=x,则BC=2-x
∵点B在线段AC上的黄金分割点,且AB>BC,
∴$\frac{AB}{AC}$=$\frac{BC}{AB}$,
可列方程为:$\frac{x}{2}$=$\frac{2-x}{x}$,
解得:x1=-1+$\sqrt{5}$,x2=-1-$\sqrt{5}$,
∴AB的长为:-1+$\sqrt{5}$;
故答案为:$\frac{AB}{AC}$=$\frac{BC}{AB}$,$\frac{x}{2}$=$\frac{2-x}{x}$,x1=-1+$\sqrt{5}$,x2=-1-$\sqrt{5}$,-1+$\sqrt{5}$;
②作图见下图1:
(2)①证明:解关于x的方程x2+2mx=n2:
x2+2mx+m2=m2+n2
(x+m)2═m2+n2,
∵t是关于x的方程x2+2mx=n2的一正实数根,
∴(t+m)2=m2+n2;
②作图见下图
点评 本题考查了:黄金分割、解一元一次方程、勾股定理等知识点,解题的关键是掌握以上知识点的内涵及其应用方法.

练习册系列答案
相关题目
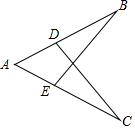 (1)如图,已知∠B=∠C,AD=AE,求证:BD=CE.
(1)如图,已知∠B=∠C,AD=AE,求证:BD=CE.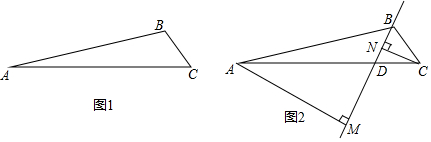
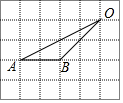 如图,正方形网格中每个小正方形的边长均为1,点A、B、O都在格点上,则∠OAB的余弦值是$\frac{2\sqrt{5}}{5}$.
如图,正方形网格中每个小正方形的边长均为1,点A、B、O都在格点上,则∠OAB的余弦值是$\frac{2\sqrt{5}}{5}$.