题目内容
10.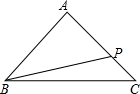 如图,在△ABC中,AB=AC=10,BC=12,若点P在边AC上移动,则BP的最小值是9.6.
如图,在△ABC中,AB=AC=10,BC=12,若点P在边AC上移动,则BP的最小值是9.6.
分析 过点A作AE⊥BC,垂足为E,过点B作BD⊥AC,垂足为D,首先由等腰三角形三线合一可知BE=6,在Rt△AEB中,由勾股定理可求得AE=8,然后利用等面积法即可求得BD的长.
解答 解:如图,过点A作AE⊥BC,垂足为E,过点B作BD⊥AC,垂足为D.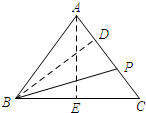
∵AC=AC,AE⊥BC,
∴BE=EC=6,
在Rt△AEB中,$AE=\sqrt{A{B}^{2}-B{E}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
由三角形的面积公式可知:$\frac{1}{2}CB•AE=\frac{1}{2}AC•BD$,即:$\frac{1}{2}×12×8=\frac{1}{2}×10×BD$,
∴BD=9.6.
故答案为:9.6.
点评 本题主要考查的是等腰三角形的性质、勾股定理以及垂线段的性质,利用等面积法求得BD的长是解题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
1.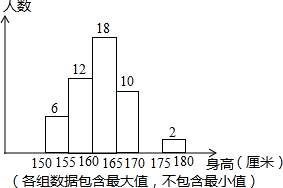 如图是初一某班全体50位同学身高情况的频数分布直方图,则身高在160-165厘米的人数的频率是( )
如图是初一某班全体50位同学身高情况的频数分布直方图,则身高在160-165厘米的人数的频率是( )
 如图是初一某班全体50位同学身高情况的频数分布直方图,则身高在160-165厘米的人数的频率是( )
如图是初一某班全体50位同学身高情况的频数分布直方图,则身高在160-165厘米的人数的频率是( )| A. | 0.36 | B. | 0.46 | C. | 0.56 | D. | 0.6 |
5. 如图,有两棵树,一棵高10m,另一棵高5m,两树相距12m,一只鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行( )
如图,有两棵树,一棵高10m,另一棵高5m,两树相距12m,一只鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行( )
 如图,有两棵树,一棵高10m,另一棵高5m,两树相距12m,一只鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行( )
如图,有两棵树,一棵高10m,另一棵高5m,两树相距12m,一只鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行( )| A. | 5m | B. | 10m | C. | 13m | D. | 17m |
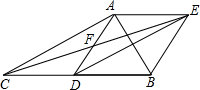 如图,在△ABC中,点D是BC的中点,点F是AD的中点,过点D作DE∥AC,交CF的延长线于点E,连接BE,AE.
如图,在△ABC中,点D是BC的中点,点F是AD的中点,过点D作DE∥AC,交CF的延长线于点E,连接BE,AE.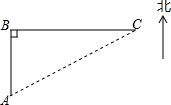 如图,在海上观察所A处,我边防海警发现正北60海里的B处,有一可疑船只正在往正东方向80海里的C处行驶,速度为40海里/小时,我边防海警立即派海警船从A处出发,沿AC方向行驶前往C处拦截,当可疑船只行驶到C处时,海警船也同时到达并将其截住,求海警船的速度.
如图,在海上观察所A处,我边防海警发现正北60海里的B处,有一可疑船只正在往正东方向80海里的C处行驶,速度为40海里/小时,我边防海警立即派海警船从A处出发,沿AC方向行驶前往C处拦截,当可疑船只行驶到C处时,海警船也同时到达并将其截住,求海警船的速度.
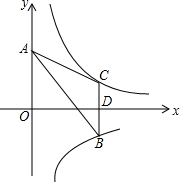 如图.两双曲线y=$\frac{k}{x}$与y=-$\frac{6}{x}$分别位于第一、第四象限,A是y轴上任意一点,B是y=-$\frac{6}{x}$上的点,C是y=$\frac{k}{x}$上的点,线段BC⊥x轴于点D,且3BD=2CD,则△ABC的面积为$\frac{15}{2}$.
如图.两双曲线y=$\frac{k}{x}$与y=-$\frac{6}{x}$分别位于第一、第四象限,A是y轴上任意一点,B是y=-$\frac{6}{x}$上的点,C是y=$\frac{k}{x}$上的点,线段BC⊥x轴于点D,且3BD=2CD,则△ABC的面积为$\frac{15}{2}$.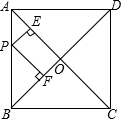 如图,正方形ABCD中,对角线BD长为15cm.P是线段AB上任意一点,则点P到AC,BD的距离之和等于$\frac{15}{2}$cm.
如图,正方形ABCD中,对角线BD长为15cm.P是线段AB上任意一点,则点P到AC,BD的距离之和等于$\frac{15}{2}$cm.