题目内容
18.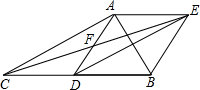 如图,在△ABC中,点D是BC的中点,点F是AD的中点,过点D作DE∥AC,交CF的延长线于点E,连接BE,AE.
如图,在△ABC中,点D是BC的中点,点F是AD的中点,过点D作DE∥AC,交CF的延长线于点E,连接BE,AE.(1)求证:四边形ACDE是平行四边形;
(2)若AB=AC,试判断四边形ADBE的形状,并证明你的结论.
分析 (1)首先证明△AFC≌△DFE,根据全等三角形对应边相等可得AC=DE,再根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)首先证明四边形ADBE为平行四边形,再根据等腰三角形的性质可得AD⊥CB,进而可得四边形ADBE为矩形.
解答 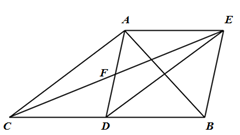 (1)证明:∵DE∥AC,
(1)证明:∵DE∥AC,
∴∠CAF=∠EDF,
∵点F是AD的中点,
∴FA=DF,
在△AFC和△DFE中
$\left\{\begin{array}{l}{∠AFC=∠DFE}\\{FA=FD}\\{∠CAF=∠EDF}\end{array}\right.$
∴△AFC≌△DFE(ASA),
∴AC=DE,
∴四边形ACDE是平行四边形;
(2)解:四边形ADBE为矩形,理由如下:
∵四边形ACDE是平行四边形,
∴AE=CD且AE∥CB,
∵点D是BC的中点,
∴CD=DB,
∴AE=BD且AE∥DB,
∴四边形ADBE为平行四边形,
又∵AB=AC,
∴AD⊥CB,
∴∠ADB=90°,
∴四边形ADBE为矩形.
点评 此题主要考查了平行四边形的判定和性质,以及矩形的判定,关键是掌握一组对边平行且相等的四边形是平行四边形;有一个角是直角的平行四边形是矩形.

练习册系列答案
相关题目
9.一元二次方程x2=2x的根是( )
| A. | x=0 | B. | x=2 | C. | x1=0,x2=2 | D. | 无实数根 |
13.抛物线y=-x2+9与y轴的交点坐标是( )
| A. | (0,9) | B. | (3,0) | C. | (-3,0) | D. | (3,0)或(3,0) |
3.下列命题中正确的是( )
| A. | 全等三角形的高相等 | B. | 全等三角形的中线相等 | ||
| C. | 全等三角形的角平分线相等 | D. | 全等三角形对应角相等 |
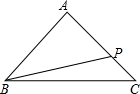 如图,在△ABC中,AB=AC=10,BC=12,若点P在边AC上移动,则BP的最小值是9.6.
如图,在△ABC中,AB=AC=10,BC=12,若点P在边AC上移动,则BP的最小值是9.6.