题目内容
20.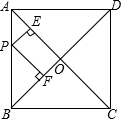 如图,正方形ABCD中,对角线BD长为15cm.P是线段AB上任意一点,则点P到AC,BD的距离之和等于$\frac{15}{2}$cm.
如图,正方形ABCD中,对角线BD长为15cm.P是线段AB上任意一点,则点P到AC,BD的距离之和等于$\frac{15}{2}$cm.
分析 作PE⊥OA于E,PF⊥OB于F,连结OP,如图,先根据正方形的性质得OA=OC=OB=OD=$\frac{1}{2}$BD=$\frac{15}{2}$,OA⊥OB,然后根据三角形面积公式得到$\frac{1}{2}$PE•OA+$\frac{1}{2}$PF•OB=$\frac{1}{2}$OA•OB,则变形后可得PE+PF=OA=$\frac{15}{2}$cm.
解答 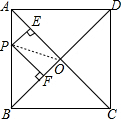 解:作PE⊥OA于E,PF⊥OB于F,连结OP,如图,
解:作PE⊥OA于E,PF⊥OB于F,连结OP,如图,
∵四边形ABCD为正方形,
∴OA=OC=OB=OD=$\frac{1}{2}$BD=$\frac{15}{2}$,OA⊥OB,
∵S△OPA+S△OPB=S△OAB,
∴$\frac{1}{2}$PE•OA+$\frac{1}{2}$PF•OB=$\frac{1}{2}$OA•OB,
∴PE+PF=OA=$\frac{15}{2}$cm.
故答案为$\frac{15}{2}$.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.

练习册系列答案
相关题目
12.如果点G是△ABC的重心,连结AG并延长交对边BC于点D,那么S△BDG:S△BGA的值为( )
| A. | 2:3 | B. | 1:2 | C. | 1:3 | D. | 3:4 |
9.将△ABC的各顶点的横坐标分别加上3,纵坐标不变,连接所得三点组成的三角形是由△ABC( )
| A. | 自左平移3个单位长度得到的 | B. | 向右平移3个单位长度得到的 | ||
| C. | 向上平移3个单位长度得到的 | D. | 向下平移3个单位长度得到的 |
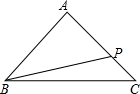 如图,在△ABC中,AB=AC=10,BC=12,若点P在边AC上移动,则BP的最小值是9.6.
如图,在△ABC中,AB=AC=10,BC=12,若点P在边AC上移动,则BP的最小值是9.6.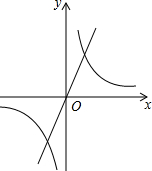 如图,已知直线y=mx与双曲线y=$\frac{k}{x}$的一个交点坐标为(3,4),则它们的另一个交点坐标是(-3,-4).
如图,已知直线y=mx与双曲线y=$\frac{k}{x}$的一个交点坐标为(3,4),则它们的另一个交点坐标是(-3,-4).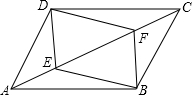 如图,已知四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接DE,BF.求证:四边形DEBF是平行四边形.
如图,已知四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接DE,BF.求证:四边形DEBF是平行四边形.