题目内容
19.用作图象的方法解方程组:$\left\{\begin{array}{l}{x+2y=-2}\\{2x+y=2}\end{array}\right.$.分析 先利用描点法画出直线x=2y=-2和直线2x+y=2,则可得到它们的交点坐标,然后根据函数图象交点坐标为两函数解析式组成的方程组的解即可得到方程组$\left\{\begin{array}{l}{x+2y=-2}\\{2x+y=2}\end{array}\right.$的解.
解答 解:如图,
直线x+2y=-2和直线2x+y=2的交点坐标为(2,-2),
所以方程组$\left\{\begin{array}{l}{x+2y=-2}\\{2x+y=2}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$.
点评 本题考查了一次函数与二元一次方程(组):函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
相关题目
8.某学校将在体育节举行跳绳活动,为此学校准备购置15米的A种跳绳与3米的B种跳绳若干,已知某商家长、短跳绳的单价如下表
(1)已知购买100条这两种跳绳共花了720元,问A种跳绳买了多少条?
(2)若该商家有一根1000米长的绳子,现将其裁成A、B两种跳绳销售,若销售总价为1300元,求销售后剩余的绳子长度.
| 跳绳种类 | A跳绳 | B跳绳 |
| 单价(单位:元) | 20 | 4 |
(2)若该商家有一根1000米长的绳子,现将其裁成A、B两种跳绳销售,若销售总价为1300元,求销售后剩余的绳子长度.
17.已知抛物线y=x2+bx+c的顶点坐标为(1,-3),则抛物线对应的函数解析式为( )
| A. | y=x2-2x+2 | B. | y=x2-2x-2 | C. | y=-x2-2x+1 | D. | y=x2-2x+1 |
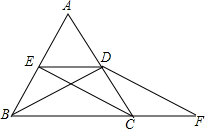 如图,已知∠ABC=∠ACB,BD平分∠ABC交AC于点D,CE平分∠ACB交AB于点E,∠DBF=∠F,问:EC与DF有怎样的位置关系?试说明理由.
如图,已知∠ABC=∠ACB,BD平分∠ABC交AC于点D,CE平分∠ACB交AB于点E,∠DBF=∠F,问:EC与DF有怎样的位置关系?试说明理由. 如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合.
如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合. 如图,五边形ABCDE和五边形JFGHI相似,求角α,β的大小和x,y,z的值.
如图,五边形ABCDE和五边形JFGHI相似,求角α,β的大小和x,y,z的值.