题目内容
9.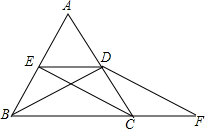 如图,已知∠ABC=∠ACB,BD平分∠ABC交AC于点D,CE平分∠ACB交AB于点E,∠DBF=∠F,问:EC与DF有怎样的位置关系?试说明理由.
如图,已知∠ABC=∠ACB,BD平分∠ABC交AC于点D,CE平分∠ACB交AB于点E,∠DBF=∠F,问:EC与DF有怎样的位置关系?试说明理由.
分析 先根据角平分线的定义得到∠DBC=$\frac{1}{2}$∠ABC,∠BCE=$\frac{1}{2}∠$ACB,加上∠ABC=∠ACB,所以∠DBC=∠BCE,由∠DBF=∠F,所以∠BCE=∠F,然后根据同位角相等,两直线平行可判断BC∥DF.
解答 解:EC∥DF.理由如下:
∵BD平分∠ABC,CE平分∠ACB,
∴∠DBC=$\frac{1}{2}$∠ABC,∠BCE=$\frac{1}{2}∠$ACB,
∵∠ABC=∠ACB,
∴∠DBC=∠BCE,
∵∠DBF=∠F,
∴∠BCE=∠F,
∴BC∥DF.
点评 本题考查了平行线判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
20.当1<m<2时,化简|m-1|-|m-2|得( )
| A. | 2m-3 | B. | -3-2m | C. | -2m-3 | D. | 3+2m |
14.已知二次函数函数y=(k-3)x2+2x-1的图象与x轴有交点,则k的取值范围是( )
| A. | k≥2 | B. | k≤2 | C. | k≥2且k≠3 | D. | k≥-4且k≠3 |
18.若x=-1是方程ax2+b=0的一个根,则方程的另一根为( )
| A. | 1 | B. | ±1 | C. | 2 | D. | -2 |
 由4个相同的小立方体搭成的几何体如图所示,则从正面看到的几何体的形状是( )
由4个相同的小立方体搭成的几何体如图所示,则从正面看到的几何体的形状是( )



 如图是一次函数y=kx+b的图象,当y>0时,x的取值范围是x<3;y≥3时,x的取值范围是x≤0.
如图是一次函数y=kx+b的图象,当y>0时,x的取值范围是x<3;y≥3时,x的取值范围是x≤0.