题目内容
2.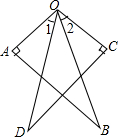 如图,OA⊥AB,OC⊥CD,OA=OC,OB=OD,求证:∠1=∠2.
如图,OA⊥AB,OC⊥CD,OA=OC,OB=OD,求证:∠1=∠2.
分析 由OA⊥AB,OC⊥CD,得到∠A=∠C=90°,证得Rt△OAC≌Rt△OCD,得到∠AOB=∠COD,于是得到结论∠1=2.
解答 证明:∵OA⊥AB,OC⊥CD,
∴∠A=∠C=90°,
在Rt△OAC与Rt△OCD中,
$\left\{\begin{array}{l}{OB=OD}\\{OA=OC}\end{array}\right.$,
∴Rt△OAC≌Rt△OCD,
∴∠AOB=∠COD,
∴∠AOB-∠DOB=∠COD-∠BOD,
即∠1=2.
点评 本题考查了直角全等三角形的判定与性质,垂直的定义,等量代换,熟记定理是解题的关键.

练习册系列答案
相关题目
10.父亲告诉小明:“距离地面越远,温度越低”,并且出示了下面的表格:
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答:
(1)如果用h(单位:km)表示距离地面的高度,用T(单位:℃)表示温度,T如何随着h的变化而变化?写出T随着h随着h变化的函数解析式;
(2)画出函数图象;
(3)你能预测出距离地面6km的高空温度是多少吗?
| 距离地面高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
| 温度(℃) | 20 | 14 | 8 | 2 | -4 | -10 |
(1)如果用h(单位:km)表示距离地面的高度,用T(单位:℃)表示温度,T如何随着h的变化而变化?写出T随着h随着h变化的函数解析式;
(2)画出函数图象;
(3)你能预测出距离地面6km的高空温度是多少吗?
7.在△ABC中,已知∠A=60°,BD⊥AC于点D,CE⊥AB于点E,且BD=CE,则△ABC是( )
| A. | 不等边三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 直角三角形 |
11.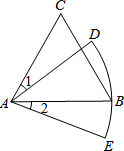 如图,△ABC是等边三角形,AC=6,以点A为圆心,AB长为半径画弧DE,若∠1=∠2,则弧DE的长为( )
如图,△ABC是等边三角形,AC=6,以点A为圆心,AB长为半径画弧DE,若∠1=∠2,则弧DE的长为( )
 如图,△ABC是等边三角形,AC=6,以点A为圆心,AB长为半径画弧DE,若∠1=∠2,则弧DE的长为( )
如图,△ABC是等边三角形,AC=6,以点A为圆心,AB长为半径画弧DE,若∠1=∠2,则弧DE的长为( )| A. | 1π | B. | 1.5π | C. | 2π | D. | 3π |
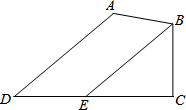 已知:如图,在四边形ABCD中,∠A=130°,∠C=90°,∠D=40°,BE∥AD交CD于点E.求证:BE平分∠ABC.
已知:如图,在四边形ABCD中,∠A=130°,∠C=90°,∠D=40°,BE∥AD交CD于点E.求证:BE平分∠ABC. 如图,小明想利用自己所学的数学知识测量连接塔AB的尖端和地面间的一条空中速滑索道AC的长度,小明先测得塔尖A在点C的北偏西22°方向,然后沿坡比为1:1(即tan∠ECD=1)的斜坡以18/分的速度步行2分钟到达E,测得点A的俯角为8°,若点A、B、C、D、E,都在同一平面内,且B、C、D三点共线.
如图,小明想利用自己所学的数学知识测量连接塔AB的尖端和地面间的一条空中速滑索道AC的长度,小明先测得塔尖A在点C的北偏西22°方向,然后沿坡比为1:1(即tan∠ECD=1)的斜坡以18/分的速度步行2分钟到达E,测得点A的俯角为8°,若点A、B、C、D、E,都在同一平面内,且B、C、D三点共线. 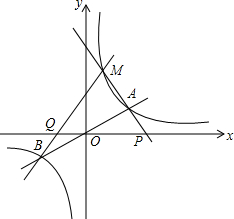 如图,已知双曲线y=$\frac{{k}_{1}+3}{x}$(k1为常数)与直线y=k2x(k2为常数)相交于A,B两点,双曲线在第一象限内部分有一点M(点M在A的左侧)在双曲线y=$\frac{{k}_{1}+3}{x}$上,设直线MA,MB分别与x轴分别交于P,Q两点.若MA=m•AP,MB=n•QB,则n-m的值是2.
如图,已知双曲线y=$\frac{{k}_{1}+3}{x}$(k1为常数)与直线y=k2x(k2为常数)相交于A,B两点,双曲线在第一象限内部分有一点M(点M在A的左侧)在双曲线y=$\frac{{k}_{1}+3}{x}$上,设直线MA,MB分别与x轴分别交于P,Q两点.若MA=m•AP,MB=n•QB,则n-m的值是2.