题目内容
已知,一次函数y=
(k是不为0的自然数,且是常数)的图象与两坐标轴所围成的图形的面积为Sk(即k=1时,得S1,k=2时,得S2,┅).试求S1+S2+S3+…+S2006的值.
| 1-kx |
| k+1 |
考点:一次函数图象上点的坐标特征
专题:规律型
分析:求出函数与坐标轴的交点,根据面积=
|x||y|可得出面积关于k的表达式,继而能得出S1+S2+S3+…+S2006的值.
| 1 |
| 2 |
解答:解:由题意得,一次函数y=
的图象与两坐标轴的交点为(
,0)、(0,
),
所围成的图形的面积为Sk=
•
=
•
.
则S1+S2+S3+…+S2006
=
•
+
•
+
•
+…+
•
=
(
+
+
+…+
)
=
(1-
+
-
+
-
+…+
-
)
=
(1-
)
=
.
| 1-kx |
| k+1 |
| 1 |
| k |
| 1 |
| k+1 |
所围成的图形的面积为Sk=
| 1 |
| 2 |
| 1 |
| k |
| 1 |
| k+1 |
| 1 |
| 2 |
| 1 |
| k(k+1) |
则S1+S2+S3+…+S2006
=
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3×4 |
| 1 |
| 2 |
| 1 |
| 2006×2007 |
=
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2006×2007 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2006 |
| 1 |
| 2007 |
=
| 1 |
| 2 |
| 1 |
| 2007 |
=
| 1003 |
| 2007 |
点评:本题考查一次函数图象上点的坐标特征与三角形的面积,有一定难度,关键是表示出Sk的表达式.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
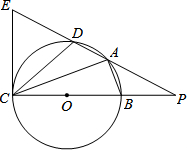 如图,已知BC为⊙O的直径,EC是⊙O的切线,C是切点,EP交⊙O于点A,D,交CB延长线于点P.连接CD,CA,AB.
如图,已知BC为⊙O的直径,EC是⊙O的切线,C是切点,EP交⊙O于点A,D,交CB延长线于点P.连接CD,CA,AB. 在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,
在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G, 已知二次函数y=-x2+2x+3图象的对称轴为直线.
已知二次函数y=-x2+2x+3图象的对称轴为直线. 列方程(组)或不等式(组)解应用题:
列方程(组)或不等式(组)解应用题: 如图,PA切⊙O于点A,OP=2,∠P=30°,弦AB∥OP.
如图,PA切⊙O于点A,OP=2,∠P=30°,弦AB∥OP.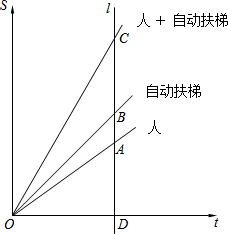 如图,直线l与x轴垂直,垂足为D,它与从原点出发的三条射线分别交于点A、B、C.射线OA、OB、OC分别表示正常行走的人,站在自动扶梯上不走的人,在自动扶梯上同时正常行走的人所移动的路程s(m)与时间t(min)的函数关系,在这些关系中,正常行走的人的速度相同,自动扶梯的速度也相同.
如图,直线l与x轴垂直,垂足为D,它与从原点出发的三条射线分别交于点A、B、C.射线OA、OB、OC分别表示正常行走的人,站在自动扶梯上不走的人,在自动扶梯上同时正常行走的人所移动的路程s(m)与时间t(min)的函数关系,在这些关系中,正常行走的人的速度相同,自动扶梯的速度也相同.