题目内容
20.已知直线y=(3m-1)x+m-1,当m为何值时(1)与y轴相交于(0,3)
(2)与x轴相交于(2,0)
(3)图象经过一、三、四象限?
分析 (1)把(0,3)代入直线解析式,求出m的值即可;
(2)(2,0)代入直线解析式,求出m的值即可;
(3)根据函数的图象的位置列出关于m的不等式,求出m的取值范围即可.
解答 解:(1)∵直线与y轴相交于点(0,3),
∴m-1=3,解得m=4;
(2)∵直线x轴相交于点(2,0),
∴2(3m-1)+m-1=0,
解得m=$\frac{3}{7}$;
(3)∵直线y=(3m-1)x+m-1图象经过一、三、四象限,
∴$\left\{\begin{array}{l}{3m-1>0}\\{m-1<0}\end{array}\right.$,
解得:$\frac{1}{3}$<m<1.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
15.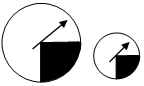 有大小两个转盘,其中黑色区域都是中心角为90°的扇形,为了探究指针落在黑色区域的频率,甲乙两人分别转动两转盘,记录下表(A:指针落在大转盘的黑色区域频数;B:大转盘中的频率;C:指针落在小转盘的黑色区域频数;D:小转盘中相应频率)
有大小两个转盘,其中黑色区域都是中心角为90°的扇形,为了探究指针落在黑色区域的频率,甲乙两人分别转动两转盘,记录下表(A:指针落在大转盘的黑色区域频数;B:大转盘中的频率;C:指针落在小转盘的黑色区域频数;D:小转盘中相应频率)
(1)将B、D两空格填写完整;
(2)分别绘出指针落在大小转盘中黑色区域的频率折线图;
(3)比较25次与50次的大小频率之差及200与225次之间大小转盘两频率之差;
(4)从(3)中频率之差及折线统计图中的变化趋势,你能总结出什么规律?
 有大小两个转盘,其中黑色区域都是中心角为90°的扇形,为了探究指针落在黑色区域的频率,甲乙两人分别转动两转盘,记录下表(A:指针落在大转盘的黑色区域频数;B:大转盘中的频率;C:指针落在小转盘的黑色区域频数;D:小转盘中相应频率)
有大小两个转盘,其中黑色区域都是中心角为90°的扇形,为了探究指针落在黑色区域的频率,甲乙两人分别转动两转盘,记录下表(A:指针落在大转盘的黑色区域频数;B:大转盘中的频率;C:指针落在小转盘的黑色区域频数;D:小转盘中相应频率)| 次数 | 25 | 50 | 75 | 100 | 125 | 150 | 175 | 200 | 225 |
| A | 8 | 15 | 21 | 26 | 32 | 36 | 44 | 51 | 57 |
| B | 0.32 | 0.30 | 0.28 | 0.26 | 0.256 | 0.24 | 0.251 | 0.255 | 0.253 |
| C | 8 | 13 | 21 | 26 | 32 | 37 | 43 | 49 | 55 |
| D | 0.32 | 0.26 | 0.28 | 0.26 | 0.256 | 0.247 | 0.246 | 0.245 | 0.244 |
(2)分别绘出指针落在大小转盘中黑色区域的频率折线图;
(3)比较25次与50次的大小频率之差及200与225次之间大小转盘两频率之差;
(4)从(3)中频率之差及折线统计图中的变化趋势,你能总结出什么规律?

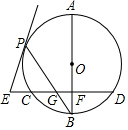 如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的反向延长线上,EP是⊙O的切线,
如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的反向延长线上,EP是⊙O的切线,