题目内容
5.已知某商品的进价为每件40元,现在的售价是每件60元,每星期可卖出300件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件.若商场规定试销期间获利不得低于40%又不得高于60%,则销售单价定为多少时,商场可获得最大利润?最大利润是多少?分析 设每星期所获利润为y,然后讨论:若销售单价x元,根据一星期利润等于每件的利润×销售量分别得到y=(x-40)[300-10(x-60)](60≤x≤90)或y=(x-40)[300+20(60-x)](0≤x≤20),然后根据获利不得低于40%又不得高于60%求出自变量的取值范围,根据二次函数的性质即可得到答案.
解答 解:∵获利不得低于40%又不得高于60%,
∴$\left\{\begin{array}{l}{x-40≥40%×40}\\{x-40≤60%×40}\end{array}\right.$,
解得:56≤x≤64,
设销售单价为x元时获得的总利润为y元.
涨价时,
y=(x-40)[300-10(x-60)](60≤x≤90)
=(x-40)(900-10x)
=-10x2+1300x-36000
=-10(x2-130x)-36000
=-10(x-65)2+6250,
当60≤x≤64时,x=64,y的最大值是6150,
降价时,
y=(x-40)[300+20(60-x)](40≤x≤60),
=(x-40)(1500-20x)
=-20x2+2300x-60000
=-20(x-57.5)2+6125,
当56≤x≤60时,x=57.5,y的最大值是6125,
综合以上两种情况,定价为64元时可获得最大利润为6150元.
点评 本题主要考查了二次函数的应用,根据题意列出函数表达式是解决问题的关键,根据自变量的取值范围运用函数的性质求最值是本题难点.

练习册系列答案
相关题目
15.“十•一”黄金周期间,西安大唐芙蓉园在7天假期中每天接待游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数).
(1)若9月30日的游客人数为a万人,则10月2日的游客人数为a+2.4万人;
(2)七天内游客人数最大的是10月3日;
(3)若9月30日游客人数为3万人,门票每人120元.请求出黄金周期间西安大唐芙蓉园门票总收入是多少万元?
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化 (万人) | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.4 |
(2)七天内游客人数最大的是10月3日;
(3)若9月30日游客人数为3万人,门票每人120元.请求出黄金周期间西安大唐芙蓉园门票总收入是多少万元?
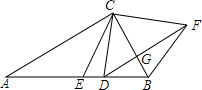 已知:△ABC中,∠ACB=90°,CE是中线,D是AB上的-点,过D作DF∥AC,过B作BF∥EC,DF、BF相交于F.连结CD、CF,求证:CD=CF.
已知:△ABC中,∠ACB=90°,CE是中线,D是AB上的-点,过D作DF∥AC,过B作BF∥EC,DF、BF相交于F.连结CD、CF,求证:CD=CF.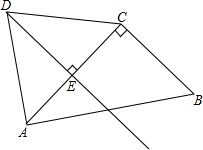 四边形ABCD中,AD=CD,AB=15,AC=12,BC=9,∠ACB=90°.
四边形ABCD中,AD=CD,AB=15,AC=12,BC=9,∠ACB=90°.
 如图,已知l1∥l2∥l3,如果AB:BC=2:3,DE=4,则EF的长是6.
如图,已知l1∥l2∥l3,如果AB:BC=2:3,DE=4,则EF的长是6.