题目内容
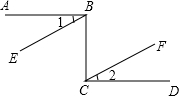
5. 如图,CD⊥AB,EF⊥AB,垂足分别为D,F,∠1=∠2=50°.
如图,CD⊥AB,EF⊥AB,垂足分别为D,F,∠1=∠2=50°.(1)求∠BCD的大小;
(2)试判断DG与BC的位置关系,并说明理由;
(3)若∠A=60°,求∠AGD的度数.
分析 (1)根据垂直于同一条直线的两直线平行,先判定EF∥CD,根据两直线平行同位角相等,得∠1=∠DCB;
(2)结合已知,根据等量代换可得∠DCB=∠2,从而根据内错角相等,两直线平行得证;
(3)根据三角形内角和定理,可得∠B的度数,再根据平行线的性质得出∠ADG的度数,进而得到∠AGD的度数.
解答 证明:(1)∵CD⊥AB,EF⊥AB,
∴EF∥CD,
∴∠1=∠DCB=50°;
(2)∵∠1=∠DCB,∠1=∠2,
∴∠2=∠BCD,
∴DG∥BC;
(3)∵∠1=50°,EF⊥AB,
∴∠B=40°,
∵DG∥BC,
∴∠ADG=∠B=40°,
又∵∠A=60°,
∴∠AGD=180°-∠ADG-∠A=80°.
点评 本题主要考查了平行线的判定与性质,由角的数量关系判断两直线的位置关系,由平行关系来寻找角的数量关系是解答此题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
 某单位有一块四边形的空地,∠B=90°,量得各边的长度AB=3米,BC=4米,CD=12米,AD=13米,现计划在空地内种草.
某单位有一块四边形的空地,∠B=90°,量得各边的长度AB=3米,BC=4米,CD=12米,AD=13米,现计划在空地内种草.
 如图,从下列条件中:
如图,从下列条件中: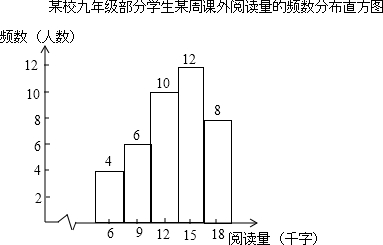 为了解九年级学生每周的课外阅读情况,某校语文组调查了该校九年级部分学生某周的课外阅读量(精确到千字),将调查数据经过统计整理后,得到如下频数分布直方图.请根据该频数分布直方图,回答下列问题:
为了解九年级学生每周的课外阅读情况,某校语文组调查了该校九年级部分学生某周的课外阅读量(精确到千字),将调查数据经过统计整理后,得到如下频数分布直方图.请根据该频数分布直方图,回答下列问题: 如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.
如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.