题目内容
16.以点A(0,2)为圆心,3为半径的圆,与x轴的交点坐标是($\sqrt{5}$,0),(-$\sqrt{5}$,0),与y轴的交点坐标是(0,-1),(0,5).分析 根据勾股定理,可得与x轴的交点坐标;根据有理数的加法,可得与y轴的交点坐标.
解答 解:由勾股定理,得
$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$,
即点A(0,2)为圆心,3为半径的圆,与x轴的交点坐标是($\sqrt{5}$,0),(-$\sqrt{5}$,0);
由有理数的加法,得
2+3=5,2-3=-1,
即点A(0,2)为圆心,3为半径的圆,与y轴的交点坐标是(0,-1),(0,5);
故答案为:($\sqrt{5}$,0),(-$\sqrt{5}$,0);(0,-1),(0,5).
点评 本题考查了坐标与图形的性质,利用勾股定理得出与x轴的交点坐标是解题关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
6.下列命题是真命题的是( )
| A. | 不相交的两条直线叫做平行线 | |
| B. | 经过直线外一点,有且只有一条直线与已知直线平行 | |
| C. | 两直线平行,同旁内角相等 | |
| D. | 两条直线被第三条直线所截,同位角相等 |
7.已知抛物线y=ax2+bx+c的开口向上,顶点坐标为(3,-2),那么该抛物线有( )
| A. | 最小值-2 | B. | 最大值-2 | C. | 最小值3 | D. | 最大值3 |
1.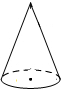 如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )
如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )
 如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )
如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )| A. | 圆锥的底面半径为3 | B. | tanα=$\frac{\sqrt{2}}{2}$ | ||
| C. | 圆锥的表面积为12π | D. | 该圆锥的主视图的面积为8$\sqrt{2}$ |
6.已知3x=5,9y=10,则3x+2y=( )
| A. | 50 | B. | -100 | C. | 100 | D. | 无法确定 |