题目内容
抛物线y=3x2,y=-3x2,y=
x2+3共有的性质是( )
| 1 |
| 3 |
| A、开口向上 |
| B、对称轴是y轴 |
| C、都有最高点 |
| D、y随x值的增大而增大 |
考点:二次函数的性质
专题:
分析:根据二次函数的性质分别分析解题即可.
解答:解:(1)y=3x2开口向上,对称轴为y轴,有最低点,顶点为原点;
(2)y=-3x2开口向下,对称轴为y轴,有最高点,顶点为原点;
(3)y=
x2+3开口向上,对称轴为y轴,有最低点,顶点为(0,3).
故选:B.
(2)y=-3x2开口向下,对称轴为y轴,有最高点,顶点为原点;
(3)y=
| 1 |
| 3 |
故选:B.
点评:此题主要考查了二次函数顶点式y=a(x-h)2+k的性质,正确把握相关性质是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下面哪个点在函数y=-x-2的图象上( )
| A、(3,0) |
| B、(0.5,2) |
| C、(-5,3) |
| D、(1,1) |
下列事件中是必然事件的是( )
| A、抛出一枚硬币,落地后正面向上 |
| B、明天太阳从西边升起 |
| C、实心铁球投入水中会沉入水底 |
| D、NBA篮球队员在罚球线投篮2次,至少投中一次 |
二次函数y=-2x2+1的图象上有两点P1(x1,y1),P2(x2,y2),当0<x1<x2时,则y1,y2的大小关系是( )
| A、y1>y2 |
| B、y1<y2<0 |
| C、y1>y2>0 |
| D、y1<y2 |
 如图,在平面直角坐标系xOy中,已知AD平分∠OAB,DB⊥AB,BC∥OA,点D的坐标为D(0,
如图,在平面直角坐标系xOy中,已知AD平分∠OAB,DB⊥AB,BC∥OA,点D的坐标为D(0,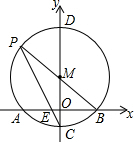 如图,在平面直角坐标系中,以M(0,2)圆心,4为半径的⊙M交x轴于A、B两点,交y轴于C、D两点,连结BM并延长交⊙M于点P,连结PC交x轴于点E.
如图,在平面直角坐标系中,以M(0,2)圆心,4为半径的⊙M交x轴于A、B两点,交y轴于C、D两点,连结BM并延长交⊙M于点P,连结PC交x轴于点E.